题目内容
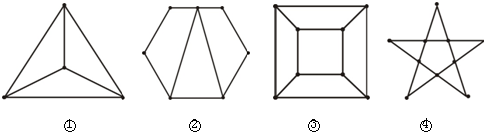
数一数图中，各有多少条线段？
分析：（1）每一条边上有2个分点，依此可得图中一条边有多少条线段，再用一条边上线段的条数×7即可求解；
（2）分横向和纵向两种情况讨论求得图中有多少条线段．
（2）分横向和纵向两种情况讨论求得图中有多少条线段．
解答：解：（1）（3+2+1）×7=42（条）．
答：有42条线段；
（2）（6+5+4+3+2+1）×4+（4+3+2+1）×7，
=21×4+10×7，
=84+70，
=154（条）．
答：有154条线段．
答：有42条线段；
（2）（6+5+4+3+2+1）×4+（4+3+2+1）×7，
=21×4+10×7，
=84+70，
=154（条）．
答：有154条线段．
点评：本题考查了线段的定义，图（2）要注意分两类查找．
练习册系列答案
相关题目
数一数图中，各有多少条线段，各有多少个三角形？
如图，①②③④四个图都称作平面图，观察图①和表中对应数值，探究计数的方法并作答．
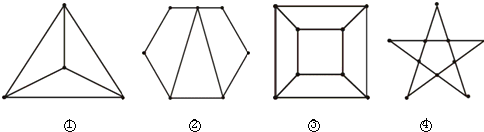
（1）数一数，每个图各有多少个顶点，多少条边，这些边围出多少区域，并将结果填入下表：
| 图 | ① | ② | ③ | ④ |
| 顶点数m | 4 | 7 | ||
| 边数n | 6 | 9 | ||
| 区域数f | 3 |
（3）如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系，则这个平面有________条边．