题目内容
 如图中,E,F,G,H均为各自所在边的三等分点.如果正方形ABCD的面积是
如图中,E,F,G,H均为各自所在边的三等分点.如果正方形ABCD的面积是| 3 |
| 4 |
| 5 |
| 12 |
| 5 |
| 12 |
分析:如图作出辅助线,则把这个正方形分成四个小长方形和内部的一个小正方形,根据E、F、G、H分别为三等分点,设正方形ABCD的边长是3a,则可得AE=BF=CG=DH=2a,则AF=BG=CH=DE=a,据此求出阴影部分1、2、3、4、5的面积之和占正方形ABCD的面积的几分之几,即可解题.


解答:解:根据题干分析可得,设正方形ABCD的边长是3a,则可得AE=BF=CG=DH=2a,则AF=BG=CH=DE=a,内部小阴影部分5的边长是a,
所以阴影部分的面积等于:2a×a÷2×4+a×a
=4a2+a2
=5a2
正方形ABCD的面积是:3a×3a=9a2
所以阴影部分的面积占正方形ABCD的面积的:5a2÷9a2=
所以阴影部分的面积是:
×
=
(平方厘米)
答:正方形EFGH的面积是
平方厘米.
故答案为:
.
所以阴影部分的面积等于:2a×a÷2×4+a×a
=4a2+a2
=5a2
正方形ABCD的面积是:3a×3a=9a2
所以阴影部分的面积占正方形ABCD的面积的:5a2÷9a2=
| 5 |
| 9 |
所以阴影部分的面积是:
| 3 |
| 4 |
| 5 |
| 9 |
| 5 |
| 12 |
答:正方形EFGH的面积是
| 5 |
| 12 |
故答案为:
| 5 |
| 12 |
点评:解答此题的关键是作出辅助线,把阴影部分的面积分在四个小长方形和中间的一个正方形中,求出阴影部分占大正方形的面积的几分之几是解决本题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD的两组对边的交点为E、F,对角线的交点为G,从A、B、C、D、E、F、G七个点中取出三个点作为三角形的顶点,试问能够作成多少个三角形.
如图,四边形ABCD的两组对边的交点为E、F,对角线的交点为G,从A、B、C、D、E、F、G七个点中取出三个点作为三角形的顶点,试问能够作成多少个三角形.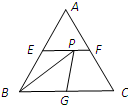 如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是
如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是 如图,长方形ABCD中,E,F,G分别是BC,CD,DA边上的中点,已知长方形ABCD的面积是30平方厘米,求阴影部分的面积.
如图,长方形ABCD中,E,F,G分别是BC,CD,DA边上的中点,已知长方形ABCD的面积是30平方厘米,求阴影部分的面积. 在边长为96厘米的正方形ABCD中(如图),E,F,G为BC上的四等分点,M,N,P为AC上的四等分点,求阴影部分的面积是多少?
在边长为96厘米的正方形ABCD中(如图),E,F,G为BC上的四等分点,M,N,P为AC上的四等分点,求阴影部分的面积是多少?