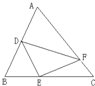
题目内容
 如图,BE=
如图,BE=| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)先看△AEC和△ABC的面积关系:BC边上的高,既是△AEC的高也是△ABC的高,已知BE=
BC,则EC=
BC,根据三角形的面积公式可得:△AEC是△ABC的面积的
;
(2)同理,可以推理出△AED和△AEC的面积关系是:△AED是△AEC的面积的
;由上述两个结论即可解决问题.
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(2)同理,可以推理出△AED和△AEC的面积关系是:△AED是△AEC的面积的
| 3 |
| 4 |
解答:解:(1)已知BE=
BC,则EC=
BC,
根据三角形面积公式可得:△AEC是△ABC的面积的
;
(2)已知CD=
AC,则AD=
AC,
根据三角形面积公式可得:△AED是△AEC的面积的
;
所以△AED=
△AEC=
×
△ABC=
△ABC.
答:三角形AED的面积是三角形ABC面积的
.
故答案为:
.
| 1 |
| 3 |
| 2 |
| 3 |
根据三角形面积公式可得:△AEC是△ABC的面积的
| 2 |
| 3 |
(2)已知CD=
| 1 |
| 4 |
| 3 |
| 4 |
根据三角形面积公式可得:△AED是△AEC的面积的
| 3 |
| 4 |
所以△AED=
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
答:三角形AED的面积是三角形ABC面积的
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题是考查了高相等的情况下,三角形的面积与这条高所在的底成正比关系的灵活应用.

练习册系列答案
相关题目
 (2008?楚州区)在如图△ABC中,AD=
(2008?楚州区)在如图△ABC中,AD=