题目内容
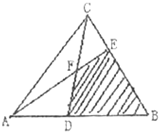 如图所示,BE=2EC,CF=FD,阴影部分的面积是三角形ABC面积的
如图所示,BE=2EC,CF=FD,阴影部分的面积是三角形ABC面积的十二
十二
分之五
五
.分析:如图所示,连接BF,因为BE=2EC,即EC:BE=1:2,所以S△AEC=
S△ABC,S△ABE=
S△ABC,又因S△CEF=
S△BEF=
S△DBF,S△ADF=S△AFC,S△DBF=S△BFC,所以S△ACF+S△BFC=
S△ABC,S△BEF=
S△ABC-
S△ABC=
S△ABC,而S△BEF:S△DBF=2:3,则S△DBF=
S△ABC,于是可以用S△ABC表示出阴影部分的面积,进而问题得解.

| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 4 |

解答:解:连接BF,因为BE=2EC,即EC:BE=1:2,
所以S△AEC=
S△ABC,S△ABE=
S△ABC,
又因S△CEF=
S△BEF=
S△DBF,S△ADF=S△AFC,S△DBF=S△BFC,
所以S△ACF+S△BFC=
S△ABC,S△BEF=
S△ABC-
S△ABC=
S△ABC,
而S△BEF:S△DBF=2:3,则S△DBF=
S△ABC,
所以阴影部分的面积为:
S△ABC+
S△ABC=
S△ABC;
答:阴影部分的面积是三角形ABC面积的
.
故答案为:十二、五.
所以S△AEC=
| 1 |
| 3 |
| 2 |
| 3 |
又因S△CEF=
| 1 |
| 2 |
| 1 |
| 3 |
所以S△ACF+S△BFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
而S△BEF:S△DBF=2:3,则S△DBF=
| 1 |
| 4 |
所以阴影部分的面积为:
| 1 |
| 6 |
| 1 |
| 4 |
| 5 |
| 12 |
答:阴影部分的面积是三角形ABC面积的
| 5 |
| 12 |
故答案为:十二、五.
点评:此题较难,应结合题意,认真审题,明确题中的数量关系,作出辅助线,根据三角形面积的有关知识解答即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
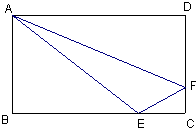 如图所示,在长方形ABCD中,△ABE、△ADF和四边形AECF的面积都相等,且BE=8,则EC的长为( )
如图所示,在长方形ABCD中,△ABE、△ADF和四边形AECF的面积都相等,且BE=8,则EC的长为( ) 如图所示,已知AD=CE,AD和BE平行,F是CD和AE的中点,则梯形ABCD的面积
如图所示,已知AD=CE,AD和BE平行,F是CD和AE的中点,则梯形ABCD的面积 如图所示,BE=2EC、FC=FD,△ABC的面积是12平米厘米,那么四边形DBEF的面积是
如图所示,BE=2EC、FC=FD,△ABC的面积是12平米厘米,那么四边形DBEF的面积是