题目内容
 如图阴影部分的面积等于三角形ABC面积的
如图阴影部分的面积等于三角形ABC面积的| 1 |
| 4 |
| 2 |
| 9 |
①
①
的面积较小.分析:空白部分①和②加上重叠部分分别是三角形和长方形,所以比较①和②的面积,只要比较三角形的面积和长方形的面积的大小即可;因为三角形ABC面积的
,等于长方形EDGF面积的
,所以:三角形的面积×
=长方形的面积×
;根据比例的性质,得出三角形与长方形的面积比,从而得出三角形和长方形面积大小的关系,进而得解.
| 1 |
| 4 |
| 2 |
| 9 |
| 1 |
| 4 |
| 2 |
| 9 |
解答:解:因为三角形ABC面积的
,等于长方形EDGF面积的
,
所以:三角形的面积×
=长方形的面积×
;
那么三角形的面积:长方形的面积=
:
=8:9;
三角形的面积小;
①的面积=三角形的面积-重叠部分的面积;
②的面积=长方形的面积-重叠部分的面积;
所以①的面积<②的面积.
故答案为:①.
| 1 |
| 4 |
| 2 |
| 9 |
所以:三角形的面积×
| 1 |
| 4 |
| 2 |
| 9 |
那么三角形的面积:长方形的面积=
| 2 |
| 9 |
| 1 |
| 4 |
三角形的面积小;
①的面积=三角形的面积-重叠部分的面积;
②的面积=长方形的面积-重叠部分的面积;
所以①的面积<②的面积.
故答案为:①.
点评:本题解题方法灵活,可以设重叠部分的面积是1,根据分数除法的意义,分别求出三角形和长方形的面积,进而求出①和②的面积,从而得解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图中A点是三角形一条底边上的中点,空白和阴影部分的面积
如图中A点是三角形一条底边上的中点,空白和阴影部分的面积 (2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积.
(2012?中山市模拟)如图,三角形ABC是面积为46.8平方厘米的等边三角形,ABCD是平行四边形,圆的半径是6厘米,求阴影部分的面积. 如图中空白部分是两个等圆,阴影部分的面积是大圆面积的
如图中空白部分是两个等圆,阴影部分的面积是大圆面积的 如图,三个等圆的周长都是18.84厘米,求阴影部分的面积.(用最简便的方法解)
如图,三个等圆的周长都是18.84厘米,求阴影部分的面积.(用最简便的方法解)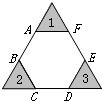 如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为
如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为