题目内容
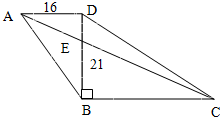 如图所示,若梯形ABCD的上底AD长16厘米,高BD长21厘米,并且BD=3DE,则三角形ADE的面积是
如图所示,若梯形ABCD的上底AD长16厘米,高BD长21厘米,并且BD=3DE,则三角形ADE的面积是56
56
平方厘米,梯形的下底BC长32
32
厘米.分析:(1)根据三角形的面积公式可以求出三角形ABD的面积是:16×21÷2=168平方厘米,又因为BD=3DE,即ED:BD=1:3,根据高一定时,三角形的面积与底成正比例的性质可得三角形ADE的面积:三角形ADB的面积=1:3,据此即可求出三角形ADE的面积;
(2)在梯形ABCD中,因为AD∥BC,所以△ADE和△CBE相似,因为BD=3DE,即DE:BE=1:2,所以AD:CB=1:2,又因为AD=16厘米,由此即可求得BC的长度.
(2)在梯形ABCD中,因为AD∥BC,所以△ADE和△CBE相似,因为BD=3DE,即DE:BE=1:2,所以AD:CB=1:2,又因为AD=16厘米,由此即可求得BC的长度.
解答:解:(1)三角形ABD的面积是:16×21÷2=168(平方厘米),
又因为BD=3DE,即ED:BD=1:3,
所以三角形ADE的面积:三角形ADB的面积=1:3,
则三角形ADE的面积是:168÷3=56(平方厘米),
(2)梯形ABCD中,因为AD∥BC,
所以△ADE和△CBE相似,
因为BD=3DE,即DE:BE=1:2,
所以AD:CB=1:2,又因为AD=16厘米,
所以CB=16×2=32(厘米),
答:三角形ADE的面积是56平方厘米,梯形的下底BC长32厘米.
故答案为:56;32.
又因为BD=3DE,即ED:BD=1:3,
所以三角形ADE的面积:三角形ADB的面积=1:3,
则三角形ADE的面积是:168÷3=56(平方厘米),
(2)梯形ABCD中,因为AD∥BC,
所以△ADE和△CBE相似,
因为BD=3DE,即DE:BE=1:2,
所以AD:CB=1:2,又因为AD=16厘米,
所以CB=16×2=32(厘米),
答:三角形ADE的面积是56平方厘米,梯形的下底BC长32厘米.
故答案为:56;32.
点评:此题主要考查高一定时,三角形的面积与底成正比例的性质以及相似三角形的对应边成比例的性质的灵活应用.

练习册系列答案
相关题目
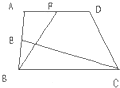 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为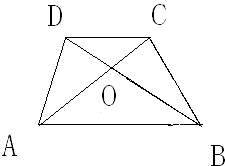 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.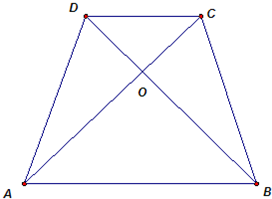 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.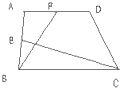 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.