Question

11．如图平行四边形中，甲的面积是48平方厘米，乙的面积占平行四边形的$\frac{1}{5}$，丙的面积是80平方厘米．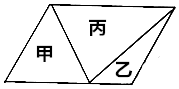

Answer 1

分析 根据图示，以及三角形面积公式可得：丙的面积=甲的面积+乙的面积，设平行四边形的面积是x，那么乙的面积就是$\frac{1}{5}$x，丙的面积=四边形面积-甲的面积-乙的面积，也就是x-48-$\frac{1}{5}$x=$\frac{4}{5}$x-48，再根据丙的面积=甲的面积+乙的面积，可列方程：48+$\frac{1}{5}$x=$\frac{4}{5}$x-48，依据等式的性质，求出x的值，再代入丙的面积即可解答．

解答 解：设平行四边形的面积是x，
丙的面积：x-48-$\frac{1}{5}$x=$\frac{4}{5}$x-48，
则  48+$\frac{1}{5}$x=$\frac{4}{5}$x-48
48+$\frac{1}{5}$x-$\frac{1}{5}$x=$\frac{4}{5}$x-48-$\frac{1}{5}$x
      48+48=$\frac{3}{5}$x-48+48，
          $\frac{3}{5}$x=96
     $\frac{3}{5}$x÷$\frac{3}{5}$=96÷$\frac{3}{5}$
             x=160
$\frac{4}{5}$×160-48
=128-48
=80（平方厘米）
答：丙的面积是80平方厘米，
故答案为：80．

点评 解答本题的关键是：明确丙的面积=甲的面积+乙的面积，用x分别表示出乙和丙的面积．