题目内容
已知
是一个四位数,且
-
=□997,方格中应填
. |
| abcd |
. |
| abcd |
. |
| dcba |
2
2
.分析:由题意得:abcd-dcba=9×(111a+10b-10c-111d),显然这个差能被9整除,因此□997要能被9整除.又因为被9整除的数,各位数字和能被9整除.也就是说□+9+9+7=□+25 能被9整除.显然□=2.
解答:解:abcd-dcba=1000a+100b+10c+d-1000d-100c-10b-a,
=999a+90b-90c-999d,
=9×(111a+10b-10c-111d),
因为9×(111a+10b-10c-111d)是9的倍数,因此abcd-dcba能被9整除,因此□997要能被9整除.
又因为被9整除的数,各位数字和能被9整除.
也就是说□+9+9+7=□+25 能被9整除.
所以,□=2.
故答案为:2.
=999a+90b-90c-999d,
=9×(111a+10b-10c-111d),
因为9×(111a+10b-10c-111d)是9的倍数,因此abcd-dcba能被9整除,因此□997要能被9整除.
又因为被9整除的数,各位数字和能被9整除.
也就是说□+9+9+7=□+25 能被9整除.
所以,□=2.
故答案为:2.
点评:此题解答的关键是根据能被9整除的数的特征,判断分析一个四位数与其反序数之差是9的倍数,进一步解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
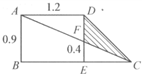
 (2005?泰州)图形计算
(2005?泰州)图形计算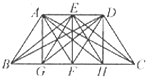 如图,已知四边形ABCD是一个等腰梯形,点E、F分别是上下两底的中点,点G、H分别是BF、CF的中点,且BC=2AD,则图中以A、B、C、D、E、F、G、H为顶点的所有三角形中,与△HEC面积相等的三角形有
如图,已知四边形ABCD是一个等腰梯形,点E、F分别是上下两底的中点,点G、H分别是BF、CF的中点,且BC=2AD,则图中以A、B、C、D、E、F、G、H为顶点的所有三角形中,与△HEC面积相等的三角形有