题目内容
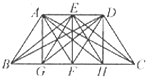 如图,已知四边形ABCD是一个等腰梯形,点E、F分别是上下两底的中点,点G、H分别是BF、CF的中点,且BC=2AD,则图中以A、B、C、D、E、F、G、H为顶点的所有三角形中,与△HEC面积相等的三角形有
如图,已知四边形ABCD是一个等腰梯形,点E、F分别是上下两底的中点,点G、H分别是BF、CF的中点,且BC=2AD,则图中以A、B、C、D、E、F、G、H为顶点的所有三角形中,与△HEC面积相等的三角形有分析:根据等底等高的三角形面积相等,分别数出以AE,DE,BG,GF,FH,CH为底的与△HEC面积相等的三角形的个数,再相加即可求解.
解答:解:以AE为底的与△HEC面积相等的三角形的个数为:5;
以DE为底的与△HEC面积相等的三角形的个数为:5;
以BG为底的与△HEC面积相等的三角形的个数为:3;
以GF为底的与△HEC面积相等的三角形的个数为:3;
以FH为底的与△HEC面积相等的三角形的个数为:3;
以CH为底的与△HEC面积相等的三角形的个数为:2;
共有与△HEC面积相等的三角形5+5+3+3+3+2=21(个).
答:与△HEC面积相等的三角形有21个.
故答案为:21.
以DE为底的与△HEC面积相等的三角形的个数为:5;
以BG为底的与△HEC面积相等的三角形的个数为:3;
以GF为底的与△HEC面积相等的三角形的个数为:3;
以FH为底的与△HEC面积相等的三角形的个数为:3;
以CH为底的与△HEC面积相等的三角形的个数为:2;
共有与△HEC面积相等的三角形5+5+3+3+3+2=21(个).
答:与△HEC面积相等的三角形有21个.
故答案为:21.
点评:考查了组合图形的计数,本题与△HEC面积相等的三角形都是等底等高的三角形.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
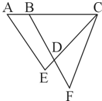 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的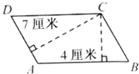 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.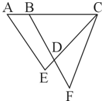 如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.
如图,已知AB=2,BC=AE=6,CE=CF=7,BF=8.则四边形ABDE的面积是△CDF面积的________倍.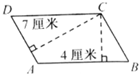 如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.
如图,已知平行四边形ABCD的周长是44厘米,AD边上的高是7厘米,AB边上的高是4厘米,求平行四边形的面积是多少平方厘米.