Question

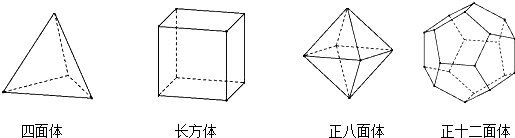
12．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：

多面体	顶点数（V）	面数（F）	棱数（E）
四面体	4	4
长方体	8	6	12
正八面体		8	12
正十二面体	20	12	30

（1）根据上面多面体模型，完成表格中的空格：
你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F-E=2；
（2）一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是20；

Answer 1

分析 （1）观察图形即可得出结论；观察可得顶点数+面数-棱数=2；
（2）代入（1）中的式子即可得到面数

解答 解：（1）观察图形，四面体的棱数为6；正八面体的顶点数为6；
观察表格可以看出：顶点数+面数-棱数=2，关系式为：V+F-E=2；

多面体	顶点数（V）	面数（F）	棱数（E）
四面体	4	4	2
长方体	8	6	12
正八面体	6	8	12
正十二面体	20	12	30

（2）由题意得：F-8+F-30=2，解得F=20．
故答案为：（1）6，6；V+F-E=2；（2）20．

点评 本题考查多面体的顶点数，面数，棱数之间的关系及灵活运用．