题目内容
17．
如图，把正三角形的每边三等分，将各边的中间段取来向外作小正三角形，得到一个六角形，再将这个六角形的六个“角”（即小正三角形）的两边三等分，又以它的中间段向外作更小的正三角形，这样就得到了如图所示的图形．如果作出的每个小三角形的面积是1，那么原图形的面积是81．
分析 
根据题意可得：每个小三角形的边长都是相等的，那么IG：AD=1：3，又因为三角形GHI和三角形AFD是相似三角形，所以S△GHI：S△AFD=1：32=1：9；同理，AD：AC=1：3，又因为三角形ABC和三角形AFD是相似三角形，所以S△AFD：S△ABC=1：32=1：9；那么S△GHI：S△ABC=1：（9×9）=1：81，再根据每个小三角形的面积是1，即可求出原图形的面积．
解答 解：每个小三角形的边长都是相等的，那么IG：AD=1：3，
又因为三角形GHI和三角形AFD是相似三角形，所以S△GHI：S△AFD=1：32=1：9；
同理，AD：AC=1：3，又因为三角形ABC和三角形AFD是相似三角形，所以S△AFD：S△ABC=1：32=1：9；
那么S△GHI：S△ABC=1：（9×9）=1：81，
又因为，S△GHI=1，
所以，原图形的面积是S△ABC=1×81=81．
故答案为：81．
点评 本题考查了相似三角形的性质的灵活应用，关键是明确相似三角形面积的比等于相似比的平方，本题体现了数形结合的规律．
练习册系列答案
阅读快车系列答案
相关题目
8．用你喜欢的方式脱式计算．
70.8-1.25-1.75
2.6+1.4×3
0.25×17.3×0.4
3.54×0.29-0.29×2.54
（8+0.8）×1.25
4.5×0.9+5.5×0.9．
70.8-1.25-1.75
2.6+1.4×3
0.25×17.3×0.4
3.54×0.29-0.29×2.54
（8+0.8）×1.25
4.5×0.9+5.5×0.9．
5．一个正方形的边长是6cm，如果把它的边长增加2cm，则面积增加（ ）cm2．
| A． | 28 | B． | 12 | C． | 4 |
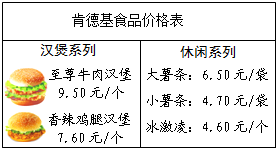去肯德基就餐．