题目内容
 如图,等边三角形ABC中,AF=2BF(即线段AF的长度是线段BF的2倍),DF=2DC、DE=2AE.若三角形ABC的面积是40.5cm2,则阴影部分面积是多少?
如图,等边三角形ABC中,AF=2BF(即线段AF的长度是线段BF的2倍),DF=2DC、DE=2AE.若三角形ABC的面积是40.5cm2,则阴影部分面积是多少?分析:因为DE=2AE,所以可得DE=
AD,则根据高一定时,三角形的面积与底成正比例的性质,可得出阴影部分的面积等于
×三角形ADF的面积;同理,因为DF=2DC、AF=2BF,可以得出三角形ADF的面积=
×三角形ACF的面积;三角形ACF的面积=
×三角形ABC的面积,则阴影部分的面积就等于
×
×
×三角形ABC的面积.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:因为DE=2AE,所以可得DE=
AD,
则阴影部分的面积=
×三角形ADF的面积;
同理,因为DF=2DC、AF=2BF
所以三角形ADF的面积=
×三角形ACF的面积;
三角形ACF的面积=
×三角形ABC的面积,
则阴影部分的面积=
×
×
×三角形ABC的面积
=
×
×
×40.5
=12(平方厘米)
答:阴影部分的面积是12平方厘米.
| 2 |
| 3 |
则阴影部分的面积=
| 2 |
| 3 |
同理,因为DF=2DC、AF=2BF
所以三角形ADF的面积=
| 2 |
| 3 |
三角形ACF的面积=
| 2 |
| 3 |
则阴影部分的面积=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
=12(平方厘米)
答:阴影部分的面积是12平方厘米.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?
如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?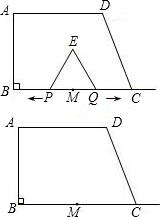
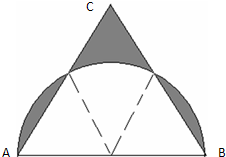 已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14)
已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14) 如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.
如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.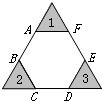 如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为
如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为