题目内容
 如图所示:三角形ABC的面积为10平方厘米,AE=DE,BD=3CD.那么阴影部分的面积是
如图所示:三角形ABC的面积为10平方厘米,AE=DE,BD=3CD.那么阴影部分的面积是3.75
3.75
平方厘米.分析:观察图形:AE=DE,BD=3CD,根据高一定时,三角形的面积与底成正比例的性质,可得:阴影部分的面积=
×三角形ABD的面积;三角形ABD的面积=
×三角形ABC的面积;由此可得阴影部分的面积=
×三角形ABC的面积,代入三角形ABC的面积即可解答问题.
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
解答:解:根据题干分析可得:阴影部分的面积=
×三角形ABD的面积;
三角形ABD的面积=
×三角形ABC的面积;
所以阴影部分的面积=
×三角形ABC的面积,
因为三角形ABC的面积是10平方厘米,
所以阴影部分的面积是:10×
=3.75(平方厘米),
答:阴影部分的面积是3.75平方厘米.
故答案为:3.75.
| 1 |
| 2 |
三角形ABD的面积=
| 3 |
| 4 |
所以阴影部分的面积=
| 3 |
| 8 |
因为三角形ABC的面积是10平方厘米,
所以阴影部分的面积是:10×
| 3 |
| 8 |
答:阴影部分的面积是3.75平方厘米.
故答案为:3.75.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
相关题目
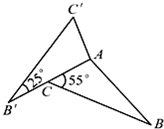 如图所示,三角形ABC按照顺时针旋转一个角度后是三角形AB?C?,已知么∠B?=25°,∠ACB=55°.旋转中心是点
如图所示,三角形ABC按照顺时针旋转一个角度后是三角形AB?C?,已知么∠B?=25°,∠ACB=55°.旋转中心是点 如图所示,三角形ABC是直角三角形,阴影①阴影的面积比阴影②的面积小28c㎡.AB长40cm,AC长是多少cm?
如图所示,三角形ABC是直角三角形,阴影①阴影的面积比阴影②的面积小28c㎡.AB长40cm,AC长是多少cm? 如图所示,三角形ABC中,D是AB边的三等分点,E是AC边的四等分点,已知三角形A DE的面积是1平方厘米.
如图所示,三角形ABC中,D是AB边的三等分点,E是AC边的四等分点,已知三角形A DE的面积是1平方厘米. 如图所示,三角形ABC是直角三角形,AB是圆的直径,并且AB=20厘米,如果阴影(Ⅰ)比阴影(Ⅱ)的面积,大7厘米,那么BC的长度是
如图所示,三角形ABC是直角三角形,AB是圆的直径,并且AB=20厘米,如果阴影(Ⅰ)比阴影(Ⅱ)的面积,大7厘米,那么BC的长度是