题目内容
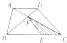 在梯形ABCD中,BE=2EC,CF=2AF,阴影部分的面积为3平方厘米,则梯形的面积为________平方厘米.
在梯形ABCD中,BE=2EC,CF=2AF,阴影部分的面积为3平方厘米,则梯形的面积为________平方厘米.
20.25
分析:在三角形BFE、三角形EFC中高相等,BE=2EC,可以求出三角形BEF的面积,在三角形BFC与三角形AFB中,高相等,CF=2AF,可以求出三角形AFB的面积,而三角形AFB的面积等于三角形DFC的面积,在三角形DFC与三角形AFD中高相等,CF=2AF,可以求出三角形ADF的面积,进而求出梯形的面积.
解答:在三角形BFE、三角形EFC中高相等,BE=2EC,
S△BEF:S△EFC=BE:EC=2:1,
S△BEF=2S△EFC=2×3=6(平方厘米),
在三角形BFC与三角形AFB中,高相等,CF=2AF,
S△ABF:S△BFC=AF:FC=1:2,
所以S△ABF= S△BFC=
S△BFC= (6+3)=4.5(平方厘米),
(6+3)=4.5(平方厘米),
S△ABF=S△DFC=4.5平方厘米,
在三角形DFC与三角形AFD中高相等,CF=2AF,
S△AFD:S△DFC=AF:FC=1:2,
所以S△AFD= S△DFC=
S△DFC= ×4.5=2.25(平方厘米),
×4.5=2.25(平方厘米),
梯形的面积是:2S△DFC+S△BEF+S△EFC+S△AFD=4.5×2+6+3+2.25=20.25(平方厘米),
故答案为:20.25.
点评:题考查了三角形的高相等时,面积与底成正比的性质的灵活应用.
分析:在三角形BFE、三角形EFC中高相等,BE=2EC,可以求出三角形BEF的面积,在三角形BFC与三角形AFB中,高相等,CF=2AF,可以求出三角形AFB的面积,而三角形AFB的面积等于三角形DFC的面积,在三角形DFC与三角形AFD中高相等,CF=2AF,可以求出三角形ADF的面积,进而求出梯形的面积.
解答:在三角形BFE、三角形EFC中高相等,BE=2EC,
S△BEF:S△EFC=BE:EC=2:1,
S△BEF=2S△EFC=2×3=6(平方厘米),
在三角形BFC与三角形AFB中,高相等,CF=2AF,
S△ABF:S△BFC=AF:FC=1:2,
所以S△ABF=
 S△BFC=
S△BFC= (6+3)=4.5(平方厘米),
(6+3)=4.5(平方厘米),S△ABF=S△DFC=4.5平方厘米,
在三角形DFC与三角形AFD中高相等,CF=2AF,
S△AFD:S△DFC=AF:FC=1:2,
所以S△AFD=
 S△DFC=
S△DFC= ×4.5=2.25(平方厘米),
×4.5=2.25(平方厘米),梯形的面积是:2S△DFC+S△BEF+S△EFC+S△AFD=4.5×2+6+3+2.25=20.25(平方厘米),
故答案为:20.25.
点评:题考查了三角形的高相等时,面积与底成正比的性质的灵活应用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
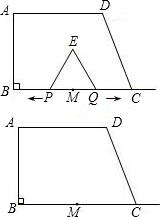
 如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0)
如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0)