题目内容
 如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0)
如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(x>0)(1)△EFG的边长是
x
x
(用含有x的代数式表示),当x=2时,点G的位置在D点
D点
;(2)若△EFG于梯形ABCD重叠部分面积是y求
①当0<x≤2时,y与x之间的函数关系式;
②当2<x≤6时,y与x之间的函数关系式.
分析:(1)根据等边三角形的三边相等,则△EFG的边长是点E移动的距离;根据等边三角形的三线合一和F点移动速度是E点移动速度的2倍,即可分析出BF=4,此时等边三角形的边长是2,则点G和点D重合;
(2)①当0<x≤2时,重叠部分的面积即为等边三角形的面积;
②当2<x≤6时,分两种情况:当2<x<3时和当3≤x≤6时,进行计算.
(2)①当0<x≤2时,重叠部分的面积即为等边三角形的面积;
②当2<x≤6时,分两种情况:当2<x<3时和当3≤x≤6时,进行计算.
解答:解:(1)因为点E、F同时从B点出发,沿射线BC向右匀速移动,且F点移动速度是E点移动速度的2倍,
所以BF=2BE=2x,
所以EF=BF-BE=2x-x=x,
所以△EFG的边长是x;
过D作DH⊥BC于H,得矩形ABHD及直角△CDH,连接DE、DF.
在直角△CDH中,因为∠C=30°,CH=BC-AD=3,
所以DH=CH?tan30°=3×
=
.
当x=2时,BE=EF=2,
因为△EFG是等边三角形,且DH⊥BC交点H,
所以EH=HF=1
所以DE=DF=
=2
所以:△DEF是等边三角形,
所以:点G的位置在D点.
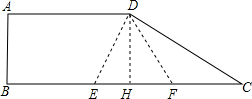
(2)①当0<x≤2时,△EFG在梯形ABCD内部,所以y=
x2;
②分两种情况:
Ⅰ.当2<x<3时,如图1,点E、点F在线段BC上,
△EFG与梯形ABCD重叠部分为四边形EFNM,
因为∠FNC=∠FCN=30°,所以FN=FC=6-2x.所以GN=3x-6.
因为在Rt△NMG中,∠G=60°,GN=3x-6,
所以GM=
(3x-6),
由勾股定理得:MN=
(3x-6),
所以S△GMN=
×GM×MN=
×
(3x-6)×
(3x-6)=
(3x-6)2,
所以,此时y=
x2-
(3x-6)2=-
x2+
x-
;
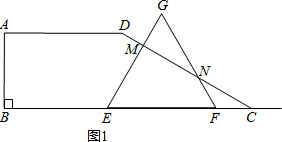
Ⅱ.当3≤x≤6时,如图2,点E在线段BC上,点F在射线CH上,
△EFG与梯形ABCD重叠部分为△ECP,
因为EC=6-x,
所以y=
(6-x)2=
x2-
x+
;
故答案为:x,D点.
所以BF=2BE=2x,
所以EF=BF-BE=2x-x=x,
所以△EFG的边长是x;
过D作DH⊥BC于H,得矩形ABHD及直角△CDH,连接DE、DF.
在直角△CDH中,因为∠C=30°,CH=BC-AD=3,
所以DH=CH?tan30°=3×
| ||
| 3 |
| 3 |
当x=2时,BE=EF=2,
因为△EFG是等边三角形,且DH⊥BC交点H,
所以EH=HF=1
所以DE=DF=
| DH2+EH2 |
所以:△DEF是等边三角形,
所以:点G的位置在D点.

(2)①当0<x≤2时,△EFG在梯形ABCD内部,所以y=
| ||
| 4 |
②分两种情况:
Ⅰ.当2<x<3时,如图1,点E、点F在线段BC上,
△EFG与梯形ABCD重叠部分为四边形EFNM,
因为∠FNC=∠FCN=30°,所以FN=FC=6-2x.所以GN=3x-6.
因为在Rt△NMG中,∠G=60°,GN=3x-6,
所以GM=
| 1 |
| 2 |
由勾股定理得:MN=
| ||
| 2 |
所以S△GMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
所以,此时y=
| ||
| 4 |
| ||
| 8 |
7
| ||
| 8 |
9
| ||
| 2 |
9
| ||
| 2 |

Ⅱ.当3≤x≤6时,如图2,点E在线段BC上,点F在射线CH上,
△EFG与梯形ABCD重叠部分为△ECP,
因为EC=6-x,
所以y=
| ||
| 8 |
| ||
| 8 |
3
| ||
| 2 |
9
| ||
| 2 |
故答案为:x,D点.
点评:此题是一道动态题,难度较大,注意不同的情况,能够熟练求得二次函数的最值.

练习册系列答案
相关题目
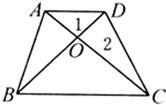 (2010?哈尔滨模拟)如图,在梯形ABCD中,AD与BC平行.已知△AOD的面积是1cm2,△DOC的面积是2cm2,那么梯形ABCD的面积是
(2010?哈尔滨模拟)如图,在梯形ABCD中,AD与BC平行.已知△AOD的面积是1cm2,△DOC的面积是2cm2,那么梯形ABCD的面积是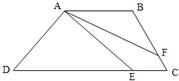 如图,在梯形ABCD中,DE=3EC,BC=3FC,四边形AECF的面积是14平方米,求梯形ABCD的面积是
如图,在梯形ABCD中,DE=3EC,BC=3FC,四边形AECF的面积是14平方米,求梯形ABCD的面积是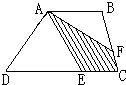 如图,在梯形ABCD中,DC=3EC,BC=3FC,四边形AECF的面积是14平方米.求梯形ABCD的面积是多少平方米?
如图,在梯形ABCD中,DC=3EC,BC=3FC,四边形AECF的面积是14平方米.求梯形ABCD的面积是多少平方米? 如图,在梯形ABCD中,对角线AC、BD相交于O点,OE平行于AB交腰BC于E点,如果三角形OBC的面积是115平方厘米,求三角形ADE的面积?
如图,在梯形ABCD中,对角线AC、BD相交于O点,OE平行于AB交腰BC于E点,如果三角形OBC的面积是115平方厘米,求三角形ADE的面积?