题目内容
 如图,在△ABC中,AB=11cm,AC=9cm.首先,在BC边上,取点H使么∠BHA=90°;然后在BC边上,在H与C之间取点D,使么BAD=60°;这样,∠DAC是∠HAD的2倍.请问,这时BH的长度是CH长度的几倍?
如图,在△ABC中,AB=11cm,AC=9cm.首先,在BC边上,取点H使么∠BHA=90°;然后在BC边上,在H与C之间取点D,使么BAD=60°;这样,∠DAC是∠HAD的2倍.请问,这时BH的长度是CH长度的几倍?分析:延长CA到E,使得AE=AB,连接BE,作AF⊥BE与F,易知∠BEA=∠EBA=∠ABH=30°+α,则直角三角形AFB和直径三角形AFE和直角三角形AHB全等,设三角形ABC的面积为1,则三角形ABE的面积为
,所以三角形AFB的面积等于三角形ABE的面积的一半,等于
,也就是三角形ABH的面积等于
,所以三角形ACH的面积等于1-
=
,所以三角形ABH的面积与三角形ACH的面积比是:
:
=
,由此得出这时BH的长度是CH长度的几倍.
| 11 |
| 9 |
| 11 |
| 18 |
| 11 |
| 18 |
| 11 |
| 18 |
| 7 |
| 18 |
| 11 |
| 18 |
| 7 |
| 18 |
| 11 |
| 7 |
解答:解:延长CA到E,使得AE=AB,连接BE,作AF⊥BE与F,
因为∠BHA=90°,∠BAD=60°,
∠DAC是∠HAD的2倍,
所以∠BEA=∠EBA=∠ABH=30°+α,
则直角三角形AFB和直径三角形AFE和直角三角形AHB全等,
设三角形ABC的面积为1,则三角形ABE的面积为
,
所以三角形AFB的面积等于三角形ABE的面积的一半,等于
,
也就是三角形ABH的面积等于
,
所以三角形ACH的面积等于1-
=
,
所以三角形ABH的面积与三角形ACH的面积比是:
:
=
,
所以BH的长度是CH长度的
倍;
答:BH的长度是CH长度的
倍.

因为∠BHA=90°,∠BAD=60°,
∠DAC是∠HAD的2倍,
所以∠BEA=∠EBA=∠ABH=30°+α,
则直角三角形AFB和直径三角形AFE和直角三角形AHB全等,
设三角形ABC的面积为1,则三角形ABE的面积为
| 11 |
| 9 |
所以三角形AFB的面积等于三角形ABE的面积的一半,等于
| 11 |
| 18 |
也就是三角形ABH的面积等于
| 11 |
| 18 |
所以三角形ACH的面积等于1-
| 11 |
| 18 |
| 7 |
| 18 |
所以三角形ABH的面积与三角形ACH的面积比是:
| 11 |
| 18 |
| 7 |
| 18 |
| 11 |
| 7 |
所以BH的长度是CH长度的
| 11 |
| 7 |
答:BH的长度是CH长度的
| 11 |
| 7 |
点评:关键是作出辅助线,利用三角形的高一定时,三角形底的比等于面积的比.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,在△ABC中,D为BC边上任一点,AE=
如图,在△ABC中,D为BC边上任一点,AE= 如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE=
如图,在△ABC中,两条角平分线CD、EF相交于F,∠A=60°,则∠DFE= (2013?北京模拟)如图,在△ABC中,AD=
(2013?北京模拟)如图,在△ABC中,AD= 如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?
如图,在△ABC中,E、D、F分别为AD、BC、AB的中点,BD=DE=EC,BF=FA,△EDF的面积是1,那么△ABC的面积是多少?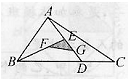 如图,在△ABC中,
如图,在△ABC中,