Question

9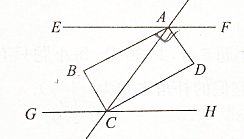．如图，已知EF∥GH，又AB，AD，CB，CD分别是∠EAC，∠FAC，∠GCA，∠HCA的平分线，若AC与EF不垂直，则图中与∠BAD相等的角是∠BCD．

Answer 1

分析 如下图所示，因为EF∥GH，由平行线的性质可知，∠EAC=∠HCA，∠FAC=∠GCA，又因为AB，AD，CB，CD分别是∠EAC，∠FAC，∠GCA，∠HCA的平分线，所以∠1=$\frac{1}{2}$∠EAC，∠2=$\frac{1}{2}$
∠HCA，因此∠1=∠2，同理可得，∠3=∠4，则∠1+∠3=∠2+∠4，即∠BAD=∠BCD，据此解答．

解答 解：如图所示：

因为EF∥GH，
所以∠EAC=∠HCA，∠FAC=∠GCA．
又因为AB，AD，CB，CD分别是∠EAC，∠FAC，∠GCA，∠HCA的平分线，
所以∠1=$\frac{1}{2}$∠EAC，∠2=$\frac{1}{2}$∠HCA，
所以∠1=∠2．
同理可得，∠3=∠4．
则∠1+∠3=∠2+∠4，
即∠BAD=∠BCD．
所以图中与∠BAD相等的角是∠BCD．
故答案为：∠BCD．

点评 本题考查了线段与角的综合，用到平行线的性质以及角平分线的定义等知识．