题目内容
若
为一个四位数,且a=d,b=c,则称这个数为四位对称数,四位对称数共有
. | abcd |
90
90
个.分析:因为a不能为0,所以d也不能为0,则a、d可以为1、2、3、4、5、6、7、8、9、共9种方法,b、c可以为0、1、2、3、4、5、6、7、8、9、共10种方法,再进行组合,看有多少方法即可.
解答:解:a不能为0,所以d也不能为0,则a、d可以为1、2、3、4、5、6、7、8、9、共9种选择方法,
b、c可以为0、1、2、3、4、5、6、7、8、9、共10选择种方法,
所以四位对称数共有9×10=90(个).
故答案为:90.
b、c可以为0、1、2、3、4、5、6、7、8、9、共10选择种方法,
所以四位对称数共有9×10=90(个).
故答案为:90.
点评:解决本题的关键是先确定a、d和b、c的取值范围,其中a、d不能为0,再进行组合即可.

练习册系列答案
相关题目
 如图,正方形ABCD的边长等于21,它被分成四个长方形:CPFN,BMFP,AQEM,DNEQ.这四个长方形的面积之比为1:2:3:4,若图中的阴影部分是一个正方形,那么这个正方形的面积是
如图,正方形ABCD的边长等于21,它被分成四个长方形:CPFN,BMFP,AQEM,DNEQ.这四个长方形的面积之比为1:2:3:4,若图中的阴影部分是一个正方形,那么这个正方形的面积是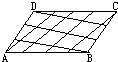 面积为5平方分米的平行四边形ABCD,若把AB、CD都平均分为四等份,把AD、BC都平均分为三等份,如图构成若干个小平行四边形,这样一个小平行四边形的面积是多少?
面积为5平方分米的平行四边形ABCD,若把AB、CD都平均分为四等份,把AD、BC都平均分为三等份,如图构成若干个小平行四边形,这样一个小平行四边形的面积是多少?