题目内容
将+,-,×,÷四个运算符号,每个各用一次,填入下面四个括号中,使该算式的值最大.
=
.
| 1 |
| 2 |
+
+
| 1 |
| 3 |
÷
÷
| 1 |
| 4 |
-
-
| 1 |
| 5 |
×
×
| 1 |
| 6 |
| 9 |
| 5 |
| 9 |
| 5 |
分析:要想算式的值最大,那就必须减去一个最小的数,而在所给的数中,只有
×
最小,所以从后向前推,最后一个运算符号为乘号,前一个运算符合为减号;又因为要保证值最大,而
又是给出的数中最大的,所以第一个运算符号为加号,由此运算符号按要求填完,计算答案即可.
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2 |
解答:解:要保证算式的值最大,
因为,
又是给出的数中最大的,所以第一个运算符号为加号,
又因为,要想算式的值最大,那就必须减去一个最小的数,
而在所给的数中,只有
×
最小,
所以从后向前推,最后一个运算符号为乘号,
前一个运算符号为减号,
由此除号的位置即可确定;
+
÷
-
×
,
=
+
-
,
=
-
,
=
,
=
,
故答案为:+,÷,-,×,
.
因为,
| 1 |
| 2 |
又因为,要想算式的值最大,那就必须减去一个最小的数,
而在所给的数中,只有
| 1 |
| 5 |
| 1 |
| 6 |
所以从后向前推,最后一个运算符号为乘号,
前一个运算符号为减号,
由此除号的位置即可确定;
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
=
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 30 |
=
| 11 |
| 6 |
| 1 |
| 30 |
=
| 54 |
| 30 |
=
| 9 |
| 5 |
故答案为:+,÷,-,×,
| 9 |
| 5 |
点评:解答此题的关键是,要保证值最大,利用逆推的方法,和运算符合的特点,先确定个别的符号的位置,再确定其它符号的位置.

练习册系列答案
相关题目
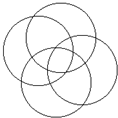 将1-13分别填入如图四个圆相互分割成的13个区域,然后把每个圆内的7个数相加,最后把四个圆的和再相加,总和最大是多少?
将1-13分别填入如图四个圆相互分割成的13个区域,然后把每个圆内的7个数相加,最后把四个圆的和再相加,总和最大是多少?