题目内容
 长方形中,△ABE和△ADF均为长方形面积的
长方形中,△ABE和△ADF均为长方形面积的| 1 | 4 |
分析:把长方形调查和宽分别看作单位“1”,根据三角形的面积公式:s=
ah,分别求出△ABR的底BE、△ADF的底DF,进而求出△CEF的面积占长方形面积的几分之几,再把长方形的面积看作单位“1”,用长方形的面积减去△ABE的面积、△ADF的面积、△CEF的面积,问题即可解决.
| 1 |
| 2 |
解答:解:已知,△ABE和△ADF均为长方形ABCD面积的
,
可得:BE=
BC,DF=
CD.
则有:△CEF的面积占长方形面积的 (1-
)×(1-
)×
=
×
×
=
,
可得:△AEF的面积占长方形面积的1-
-
-
=
;
答:△AEF的面积占长方形面积的
.
| 1 |
| 4 |
可得:BE=
| 1 |
| 2 |
| 1 |
| 2 |
则有:△CEF的面积占长方形面积的 (1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
可得:△AEF的面积占长方形面积的1-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 3 |
| 8 |
答:△AEF的面积占长方形面积的
| 3 |
| 8 |
点评:此题主要利用三角形的面积公式求出△ABR的底BE、△ADF的底DF,进而求出△CEF的面积占长方形面积的几分之几,把长方形的面积看作单位“1”,然后用单位“1”减去已知的三个三角形的面积.

练习册系列答案
相关题目
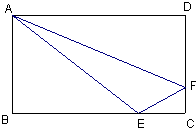 如图所示,在长方形ABCD中,△ABE、△ADF和四边形AECF的面积都相等,且BE=8,则EC的长为( )
如图所示,在长方形ABCD中,△ABE、△ADF和四边形AECF的面积都相等,且BE=8,则EC的长为( )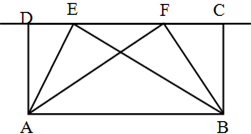 已知四边形ABCD是长方形,三角形ABE中的点E可以在线段CD上移动,如果E点移动到F上,三角形ABE和三角形ABF的面积分别为甲和乙,那么它们的大小关系是( )
已知四边形ABCD是长方形,三角形ABE中的点E可以在线段CD上移动,如果E点移动到F上,三角形ABE和三角形ABF的面积分别为甲和乙,那么它们的大小关系是( ) 已知四边形ABCD是长方形,三角形ABE中的点E可以在线段CD上移动,如果E点移动到F上,三角形ABE和三角形ABF的面积分别为甲和乙,那么它们的大小关系是
已知四边形ABCD是长方形,三角形ABE中的点E可以在线段CD上移动,如果E点移动到F上,三角形ABE和三角形ABF的面积分别为甲和乙,那么它们的大小关系是 长方形中,△ABE和△ADF均为长方形面积的
长方形中,△ABE和△ADF均为长方形面积的 ,那么,△AEF的面积占长方形面积的几分之几?
,那么,△AEF的面积占长方形面积的几分之几?