Question

图形中有

72

个三角形．

Answer 1

分析：由题图可知，这是个对称图形，我们可按以下步骤来数：

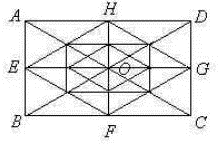
第一步：大矩形ABCD可分为四个相同的小矩形：AEOH、EBFO、OFCG、HOGD每个小矩形内所包含的三角形个数是相同的．                                                    
第二步：每两个小矩形组合成的图形共有四个，如：ABFH、EBCG、HFCD、AEGD，每个这样的图形中所包含的三角形个数是相同的．
第三步：每三个小矩形占据的部分图形共有四个：如△ABD、△ADC、△ABC、△DBC，每一个这样的图形中所包含的三角形个数是相同的．
最后把每一步中每个图形所包含三角形个数求出相加再乘以4就是整个图形中所包含的三角形的个数．

解答：解：如图：这是个对称图形，我们可按以下几个部分来数：

（1）在小矩形AEOH中：
①由一个三角形构成的8个．
②由两个三角形构成的三角形有5个．
 ③由三个或三个以上三角形构成的三角形有5个．
这样在一个小矩形内有18个三角形．
（2）在由两个小矩形组合成的图形中，如矩形AEGD，共有5个三角形．
（3）由三个小矩形占据的图形中，如△ABC，共有2个三角形．
所以整个图形中共有三角形个数是：
（18+5+2）×4=25×4=100（个）；
故填100．

点评：这是一个较为复杂的组合图形计数问题，解答技巧是：根据图形的对称你特点，把图形划分为几个部分，把各部分图中最小三角形作为基数1，然后按含有不同个数基数，分别对各部分图形中的三角形进行计数，最后求和．