题目内容
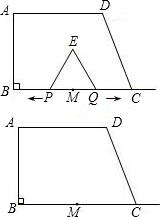
如图，一个大三角形被分成四部分，其中三个小三角形的面积分别为5，8，10．试问整个大三角形的面积是多少？分析：取OB的中点F，连接AF，利用面积相等可得出O、F是线段BE的三等分点，进而可以求出△ODE的面积，设S△DEC=S，利用三角形的面积公式得出
与△DEC的面积S的关系式，列出式子求出S的值，则四边形ODCE的面积=S+S△ODE，代入所求的值求解即可．
| BD |
| DC |
解答：解：如下图所示：取OB的中点F，连接AF、DF、DE，
易知：S△ABF=S△AFO=
S△OAB=5，
由于S△OAE=5=S△ABF=S△AFO，
由三角形的面积公式可得BF=OF=OE，
所以易知：S△ODE=S△FBD=S△FOD=
S△OBD=4，
设S△DEC=S，则：
S△ABD=S△OAB+S△OBD=10+8=18，
S△ADC=S△OAE+S△ODE+S△DEC=5+4+S=9+S，
S△BDE=S△OBD+S△ODE=8+4=12，
由三角形的面积公式可得：
=
=
，
=
=
，
即：
=
，
所以S=18，
四边形ODCE的面积=18+4=22．
所以大三角形的面积是：5+8+10+22=45，
答：大三角形的面积是45．
易知：S△ABF=S△AFO=
| 1 |
| 2 |
由于S△OAE=5=S△ABF=S△AFO，
由三角形的面积公式可得BF=OF=OE，
所以易知：S△ODE=S△FBD=S△FOD=
| 1 |
| 2 |
设S△DEC=S，则：
S△ABD=S△OAB+S△OBD=10+8=18，
S△ADC=S△OAE+S△ODE+S△DEC=5+4+S=9+S，
S△BDE=S△OBD+S△ODE=8+4=12，
由三角形的面积公式可得：
| SABD |
| SADC |
| BD |
| DC |
| 18 |
| 9+S |
| SBDE |
| SEDC |
| BD |
| DC |
| 12 |
| S |
即：
| 18 |
| 9+S |
| 12 |
| S |
所以S=18，
四边形ODCE的面积=18+4=22．
所以大三角形的面积是：5+8+10+22=45，
答：大三角形的面积是45．
点评：本题主要考查三角形面积公式的灵活应用，关键在于根据题意找出三等分点．
练习册系列答案
相关题目
如图，一个大三角形被分成了四个小三角形，其中三个三角形的面积分别是9cm2、10cm2和5cm2，那么阴影部分的面积是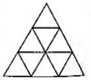
如图是一个由9个相同的小等边三角形所组成的大等边三角形．现在要把一枚黑子和一枚白子分别被放入两个小等边三角形中，并且要求这两个小等边三角形既没有公共边也没有公共顶点，那么共有