题目内容
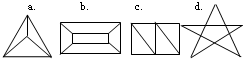
数一数，下面这个图形中，一共有多少个三角形？分析：（1）以线段FG上的各条线段为底边的三角形的个数；线段FG上共有线段5+4+3+2+1=15（条），以A为顶点，其中任何一条线段为底，均可得到一个三角形，共可得到15个三角形；
（2）同理可求出以线段DE上的各条线段为底边的三角形有15个；
（3）同理可求出以线段BC上的各条线段为底边的三角形有15个．
（2）同理可求出以线段DE上的各条线段为底边的三角形有15个；
（3）同理可求出以线段BC上的各条线段为底边的三角形有15个．
解答：解：（1）线段FG上共有线段5+4+3+2+1=15（条），以A为顶点，其中任何一条线段为底，均可得到一个三角形，共可得到15个三角形．
（2）同理可求出以线段DE上的各条线段为底边的三角形有15个；
（3）同理可求出以线段BC上的各条线段为底边的三角形有15个；
三角形一共的个数：15×3=45（个）；
答：一共有45个三角形．
（2）同理可求出以线段DE上的各条线段为底边的三角形有15个；
（3）同理可求出以线段BC上的各条线段为底边的三角形有15个；
三角形一共的个数：15×3=45（个）；
答：一共有45个三角形．
点评：对于个数较多的三角形可按规律分类灵活去做．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
