Question

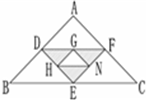如图，点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点．那么，阴影部分的面积与三角形ABC的面积比是

3：16

．

Answer 1

分析：由图及条件可知：S△DEF=S△DBE=S△EFC=S△ADF；S△GHN=S△GDH=S△HEN=S△NFG，从而可得，S△DEF=

1

4

S△ABC，S△GHN=

1

4

S△DEF，据此问题得解．

解答：解：因点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点，
所以，S△DEF=

1

4

S△ABC，S△GHN=

1

4

S△DEF，
故有S△GHN=

1

16

S△ABC，
则阴影面积=

1

4

S△ABC-

1

16

S△ABC=

3

16

S△ABC．
答：阴影部分的面积与三角形ABC的面积比是3：16．
故答案为3：16．

点评：此题主要考查三角形的面积，关键是用好等分点．