题目内容
 下图是由竖直线和水平线组成的图形,(长度单位是米),过A点画一条直线把这个图形分成面积相等的两部分,这条直线和边界相交于一点K,从A沿边界走到K点,较短的路程是________米.
下图是由竖直线和水平线组成的图形,(长度单位是米),过A点画一条直线把这个图形分成面积相等的两部分,这条直线和边界相交于一点K,从A沿边界走到K点,较短的路程是________米.
13.5
分析:先连接AD,得到两个梯形,分别算出两个梯形的面积,进行比较,梯形ABCD小于梯形ADEF的面积,所以连接的K点应在DE上,然后根据两个梯形的面积差而求出K点的位置,
最后分别计算从A沿边界走到K点的路程,找出较短者即可.
解答:SABCD=(2+6)×5÷2,
=8×5÷2,
=20(平方米);
SADEF=(3+8)×4÷2,
=11×4÷2,
=22(平方米);
SABCD<SADEF,所以K点应在DE上,
由图知,如果让两个梯形的面积相等,那么其三角形ADK的面积就应为1平方米,
因为三角形ADK的高为4米,由S三=DK×8÷2,
DK=S三×2÷4,
=1×2÷4,
=0.5(米);
沿AFEK到K点=8+4+(3-0.5),
=12+2.5,
=14.5(米);
沿ABCDK到K点=6+5+2+0.5=13.5(米);
13.5米<14.5米;
故答案为:13.5.

点评:此题考查了组合图形的面积和学生的分问题及作图能力.
分析:先连接AD,得到两个梯形,分别算出两个梯形的面积,进行比较,梯形ABCD小于梯形ADEF的面积,所以连接的K点应在DE上,然后根据两个梯形的面积差而求出K点的位置,
最后分别计算从A沿边界走到K点的路程,找出较短者即可.
解答:SABCD=(2+6)×5÷2,
=8×5÷2,
=20(平方米);
SADEF=(3+8)×4÷2,
=11×4÷2,
=22(平方米);
SABCD<SADEF,所以K点应在DE上,
由图知,如果让两个梯形的面积相等,那么其三角形ADK的面积就应为1平方米,
因为三角形ADK的高为4米,由S三=DK×8÷2,
DK=S三×2÷4,
=1×2÷4,
=0.5(米);
沿AFEK到K点=8+4+(3-0.5),
=12+2.5,
=14.5(米);
沿ABCDK到K点=6+5+2+0.5=13.5(米);
13.5米<14.5米;
故答案为:13.5.

点评:此题考查了组合图形的面积和学生的分问题及作图能力.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
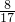 ÷9+
÷9+ ×
× -
- )×(
)×( +
+ )
) ÷[
÷[ ×(
×( +
+ )].
)].
 把一个正方体A切成两个完全一样的长方体B和C,长方体B的表面积是原正方体A表面积的________.
把一个正方体A切成两个完全一样的长方体B和C,长方体B的表面积是原正方体A表面积的________.