题目内容
已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的
,求三角形AEF的面积.

| 1 | 3 |

分析:先求出长方形ABCD的面积,再根据三角形ABE和三角形ADF的面积,各占长方形ABCD的
,可求BE、DF的长,长而得到CE、CF的长,从而得到三角形CEF的面积;三角形AEF的面积=长方形ABCD的面积-(三角形ABE的面积+三角形ADF的面积+三角形CEF的面积).
| 1 |
| 3 |
解答:解:12×8=96(平方厘米),
96×
=32(平方厘米),
32×2÷8=8(厘米),
32×2÷12=5
(厘米),
×(12-8)×(8-5
),
=
×4×
,
=5
(平方厘米),
96-(32+32+5
),
=96-69
,
=26
(平方厘米).
答:三角形AEF的面积是26
平方厘米.
96×
| 1 |
| 3 |
32×2÷8=8(厘米),
32×2÷12=5
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
=
| 1 |
| 2 |
| 8 |
| 3 |
=5
| 1 |
| 3 |
96-(32+32+5
| 1 |
| 3 |
=96-69
| 1 |
| 3 |
=26
| 2 |
| 3 |
答:三角形AEF的面积是26
| 2 |
| 3 |
点评:考查了长方形和三角形的面积计算,本题的难点是求出三角形CEF的面积.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图,矩形ABCD被分成一些正方形.已知AB=32厘米,试求AD的长度是多少?
如图,矩形ABCD被分成一些正方形.已知AB=32厘米,试求AD的长度是多少?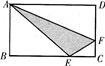 已知AB=9厘米,AD=12厘米,三角形ABE和三角形ADF的面积各占长方形ABCD的
已知AB=9厘米,AD=12厘米,三角形ABE和三角形ADF的面积各占长方形ABCD的 ,求三角形AEF的面积.
,求三角形AEF的面积.