题目内容
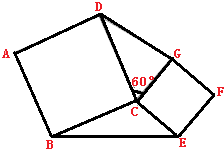 如图,已知边长为5的正方形ABCD和边长为3的正方形CEFG共顶点C,正方形CEFG绕点C旋转60°,连接BE、DG,则△BCE的面积与△CDG的面积比是
如图,已知边长为5的正方形ABCD和边长为3的正方形CEFG共顶点C,正方形CEFG绕点C旋转60°,连接BE、DG,则△BCE的面积与△CDG的面积比是1:1
1:1
.分析:(1)在△BCE中根据正弦定理,它的面积是
BC×CEsinBCE,BC是边长为5的正方形ABCD的边长,所以BC=5,CE是边长为3的正方形CEFG的边长,所以CE=3,正方形CEFG绕点C旋转60°,可求出∠BCE=120°,可求出△BCE的面积;同理在△CDG中根据正弦定理求出它的面积.据此可解答.
(2)将△CDG逆时针旋转90°,得到△CBH,H、C、E共线,△CDG与△CBH的高相等,又因CH=CE=3,根据三角形的面积公式可求出它们的比.
| 1 |
| 2 |
(2)将△CDG逆时针旋转90°,得到△CBH,H、C、E共线,△CDG与△CBH的高相等,又因CH=CE=3,根据三角形的面积公式可求出它们的比.
解答:解:(1)S△BCE=
BC×CEsinBCE=
×5×3×sin120°
S△CDG=
CD×CGsinDCG=
×5×3×sin60°
因sin120°=sin60°
S△BCE:S△CDG=(
×5×3×sin120°):(
×5×3×sin60°)=1:1
故答案为;1:1.
(2)将△CDG逆时针旋转90°,得到△CBH,H、C、E共线,△CDG与△CBH的高相等,又因CH=CE=3,根据三角形的面积公式可求出它们的比.

S△CDG=S△CBH=
×3×h
S△BCE=
×3×h
S△BCE:S△CDG=(
×3×h):(
×3×h)=1:1
故答案为1:1.
| 1 |
| 2 |
| 1 |
| 2 |
S△CDG=
| 1 |
| 2 |
| 1 |
| 2 |
因sin120°=sin60°
S△BCE:S△CDG=(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为;1:1.
(2)将△CDG逆时针旋转90°,得到△CBH,H、C、E共线,△CDG与△CBH的高相等,又因CH=CE=3,根据三角形的面积公式可求出它们的比.

S△CDG=S△CBH=
| 1 |
| 2 |
S△BCE=
| 1 |
| 2 |
S△BCE:S△CDG=(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为1:1.
点评:本题考查了学生利用正弦定理求三角形的面积,并根据比的知识来解答.在小学阶段有难度.本题还可利用旋转的方法来求,这种方法在小学阶段好.

练习册系列答案
相关题目
 如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.
如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积. 如图,有一块边长为3米的正方形草地,在点B处用一根木桩牵住了一头小羊.已知牵羊的绳子长2米,那么草地上不会被羊吃掉草的部分是
如图,有一块边长为3米的正方形草地,在点B处用一根木桩牵住了一头小羊.已知牵羊的绳子长2米,那么草地上不会被羊吃掉草的部分是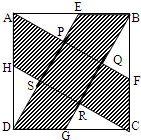 如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.
如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积. 如图,已知边长为5的正方形ABCD和边长为3的正方形CEFG共顶点C,正方形CEFG绕点C旋转60°,连接BE、DG,则△BCE的面积与△CDG的面积比是________.
如图,已知边长为5的正方形ABCD和边长为3的正方形CEFG共顶点C,正方形CEFG绕点C旋转60°,连接BE、DG,则△BCE的面积与△CDG的面积比是________.