题目内容
请问经过612个不共线的点,两两连线并向两边延长,共可以画出
186966
186966
条直线.分析:如图,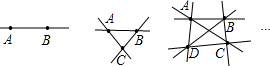
对于第n个点,可以与其它所有点作(n-1)条直线,所以共可以作出n(n-1)条直线,但每条直线都重复一次,所以共可以作
条直线.

对于第n个点,可以与其它所有点作(n-1)条直线,所以共可以作出n(n-1)条直线,但每条直线都重复一次,所以共可以作
| n(n-1) |
| 2 |
解答:解:根据题干分析可得:对于n个点,因为任意三点不在一条直线上,
所以以一点来看,它与其它所有点存在(n-1)条直线,
由于这样的点有n个,所以共有n(n-1)条,又这样每条直线重复一次,所以共有
.
当n=612时,
=186966(条),
答:共可以画出186966条直线.
故答案为:186966.
所以以一点来看,它与其它所有点存在(n-1)条直线,
由于这样的点有n个,所以共有n(n-1)条,又这样每条直线重复一次,所以共有
| n(n-1) |
| 2 |
当n=612时,
| 612×(612-1) |
| 2 |
答:共可以画出186966条直线.
故答案为:186966.
点评:每条直线都重复一次是本题容易出错的地方,需要同学们注意,另外这个公式在初中阶段经常使用,需要熟练掌握.

练习册系列答案
相关题目