题目内容
一个小球以5m/s的速度水平向左运动,碰到墙壁后经过0.2s后以2m/s的速度沿同一直线反弹.则小球在这段时间内的平均加速度为( )
|
试题答案
C
相关题目
一个小球以5m/s的速度水平向左运动,碰到墙壁后经过0.2s后以2m/s的速度沿同一直线反弹.则小球在这段时间内的平均加速度为( )
查看习题详情和答案>>
| A.15m/s2,方向向右 | B.15m/s2,方向向左 |
| C.35m/s2,方向向右 | D.35m/s2,方向向左 |
一个小球以5m/s的速度水平向左运动,碰到墙壁后经过0.2s后以2m/s的速度沿同一直线反弹.则小球在这段时间内的平均加速度为( )
A.15m/s2,方向向右
B.15m/s2,方向向左
C.35m/s2,方向向右
D.35m/s2,方向向左
查看习题详情和答案>>
A.15m/s2,方向向右
B.15m/s2,方向向左
C.35m/s2,方向向右
D.35m/s2,方向向左
查看习题详情和答案>>
一个小球以5m/s的速度水平向左运动,碰到墙壁后经过0.2s后以2m/s的速度沿同一直线反弹.则小球在这段时间内的平均加速度为
- A.15m/s2,方向向右
- B.15m/s2,方向向左
- C.35m/s2,方向向右
- D.35m/s2,方向向左
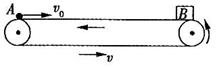
 (2009?德阳模拟)在光滑水平面上有两个可视为质点的小球A、B,mA=1kg,mB=0.5kg在两球间存在一有限区域:当两小球均在该区域内或者任一小球在该区域内两球间就有相互作用的恒定斥力F=1N,当两小球均在该区域外时两球间无作用力.A球离作用区左边界SA=20m,B在作用区右边界处,作用区长度L=5.5m.现使A以初速度vA=8m/s、B球以初速度vB=2m/s相向运动.求:
(2009?德阳模拟)在光滑水平面上有两个可视为质点的小球A、B,mA=1kg,mB=0.5kg在两球间存在一有限区域:当两小球均在该区域内或者任一小球在该区域内两球间就有相互作用的恒定斥力F=1N,当两小球均在该区域外时两球间无作用力.A球离作用区左边界SA=20m,B在作用区右边界处,作用区长度L=5.5m.现使A以初速度vA=8m/s、B球以初速度vB=2m/s相向运动.求:(1)A从开始运动到完全穿过作用区所用时间
(2)适当调节作用区的宽度或作用力大小,可使A穿过作用区后A、B两球的总动能最小,求A、B两球的最小总动能.
(09年德阳市一诊)(15分)在光滑水平面上有两个可视为质点的小球A、B,mA =1kg,mB =0.5kg在两球间存在一有限区域:当两小球均在该区域内或者任一小球在该区域内两球间就有相互作用的恒定斥力F=1N,当两小球均在该区域外时两球间无作用力。A球离作用区左边界SA=20m,B在作用区右边界处,作用区长度L=5.5m。现使A以初速度vA=8m/s、B球以初速度vB=2m/s相向运动。求:

(1)A从开始运动到完全穿过作用区所用时间;
(2)适当调节作用区的宽度或作用力大小,可使A穿过作用区后A、B两球的总动能最小,求A、B两球的最小总动能。
查看习题详情和答案>>图是一种过山车的简易模型,它由水平轨道和在竖直平面内的二个圆形轨道组成,B、C分别是二个圆形轨道的最低点,BC 间距L=12.5m,第一圆形轨道半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以V0=12.0m/s的初速度沿轨道向右运动.小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.计算结果保留小数点后一位数字.试求
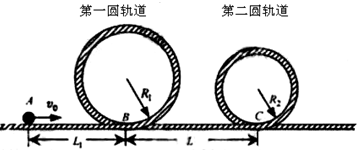
(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离.
查看习题详情和答案>>

(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离.
图是一种过山车的简易模型,它由水平轨道和在竖直平面内的二个圆形轨道组成,B、C分别是二个圆形轨道的最低点,BC 间距L=12.5m,第一圆形轨道半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以V0=12.0m/s的初速度沿轨道向右运动.小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.计算结果保留小数点后一位数字.试求

(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离.
查看习题详情和答案>>

(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离.
图是一种过山车的简易模型,它由水平轨道和在竖直平面内的二个圆形轨道组成,B、C分别是二个圆形轨道的最低点,BC 间距L=12.5m,第一圆形轨道半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以V=12.0m/s的初速度沿轨道向右运动.小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.计算结果保留小数点后一位数字.试求

(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离.
查看习题详情和答案>>

(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离.
查看习题详情和答案>>