(17)(本小题满分12分) 

如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知 ,
, ,于A处测得水深
,于A处测得水深 ,于B处测得水深
,于B处测得水深 ,于C处测得水深
,于C处测得水深 ,求∠DEF的余弦值。
,求∠DEF的余弦值。


(18)(本小题满分12分)
如图,在三棱锥 中,⊿
中,⊿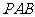 是等边三角形,∠PAC=∠PBC=90 º
是等边三角形,∠PAC=∠PBC=90 º
 (Ⅰ)证明:AB⊥PC
(Ⅰ)证明:AB⊥PC
(Ⅱ)若 ,且平面
,且平面 ⊥平面
⊥平面 ,
,
求三棱锥 体积。
体积。
(19)(本小题满分12分)
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(Ⅰ)A类工人中和B类工人各抽查多少工人?
(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
|
生产能力分组 |
 |
 |
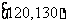 |
 |
 |
|
人数 |
4 |
8 |
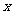 |
5 |
3 |
表2:
|
生产能力分组 |
 |
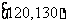 |
 |
 |
|
人数 |
6 |
y |
36 |
18 |
(1) 先确定 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)

(ii)分别估计 类工人和
类工人和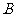 类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
(20)(本小题满分12分)
已知椭圆 的中心为直角坐标系
的中心为直角坐标系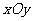 的原点,焦点在
的原点,焦点在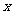 轴上,它的一个项点到两个
轴上,它的一个项点到两个
焦点的距离分别是7和1
(I)
求椭圆 的方程‘
的方程‘
(II)
若 为椭圆
为椭圆 的动点,
的动点, 为过
为过 且垂直于
且垂直于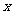 轴的直线上的点,
轴的直线上的点,
(e为椭圆C的离心率),求点 的轨迹方程,并说明轨迹是什么曲线。
的轨迹方程,并说明轨迹是什么曲线。
(21)(本小题满分12分)
已知函数 .
.
(1)
设 ,求函数
,求函数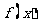 的极值;
的极值;
(2)
若 ,且当
,且当 时,
时,
 12a恒成立,试确定
12a恒成立,试确定 的取值范围.
的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分。作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。 

(22)(本小题满分10分)选修4-1;几何证明选讲
 如图,已知
如图,已知 ABC中的两条角平分线
ABC中的两条角平分线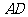 和
和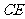 相交于
相交于 ,
, B=60
B=60 ,
,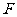 在
在 上,且
上,且 。
。 

(1)证明: 四点共圆;
四点共圆;
(2)证明:CE平分 DEF。
DEF。
(23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。
(1)化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点 到直线
到直线
 (t为参数)距离的最小值。
(t为参数)距离的最小值。 

(24)(本小题满分10分)选修4-5:不等式选讲
如图, 为数轴的原点,
为数轴的原点, 为数轴上三点,
为数轴上三点, 为线段
为线段 上的动点,设
上的动点,设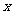 表示
表示 与原点的距离,
与原点的距离, 表示
表示 到
到 距离4倍与
距离4倍与 到
到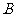 距离的6倍的和.
距离的6倍的和.
(1)将 表示为
表示为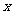 的函数;
的函数;
(2)要使 的值不超过70,
的值不超过70,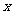 应该在什么范围内取值?
应该在什么范围内取值?



2009年普通高等学校招生全国统一考试
 ,
, ,因
,因 在区间
在区间 上不单调,所以
上不单调,所以 在
在 上有实数解,且无重根,由
上有实数解,且无重根,由


 ,令
,令 有
有 ,记
,记 则
则 在
在 上单调递减,在
上单调递减,在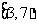 上单调递增,所以有
上单调递增,所以有 ,于是
,于是 ,得
,得 ,而当
,而当 时有
时有 ,故舍去,所以
,故舍去,所以 ;
;  时有
时有 ;
; 时有
时有 ,因为当
,因为当 时不合题意,因此
时不合题意,因此 ,
, ,B=
,B= (ⅰ)当
(ⅰ)当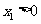 时,
时, 在
在 上单调递增,所以要使
上单调递增,所以要使 成立,只能
成立,只能 且
且 ,因此有
,因此有 ,(ⅱ)当
,(ⅱ)当 时,
时, 且
且 ,综合(ⅰ)(ⅱ)
,综合(ⅰ)(ⅱ) ;
; ,即
,即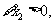 使得
使得 的值是唯一的;
的值是唯一的; ,即存在唯一的非零实数
,即存在唯一的非零实数 ,要使
,要使 所求的椭圆方程为
所求的椭圆方程为 ,
,  则抛物线
则抛物线 在点P处的切线斜率为
在点P处的切线斜率为 ,直线MN的方程为
,直线MN的方程为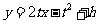 ,将上式代入椭圆
,将上式代入椭圆 的方程中,得
的方程中,得 ,即
,即 ,因为直线MN与椭圆
,因为直线MN与椭圆 ,
, ,则
,则 ,
,  ,则
,则 ,由题意得
,由题意得 ,即有
,即有 ,其中的
,其中的 或
或 ;
; ,因此不等式
,因此不等式 ,当
,当 时代入方程
时代入方程 ,将
,将 代入不等式
代入不等式 的最小值为1.
的最小值为1. 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O ,
,  则
则

 ,由题意得,
,由题意得, 因
因 ,因此平面BOE的法向量为
,因此平面BOE的法向量为 ,
, 得
得 ,又直线
,又直线 不在平面
不在平面 内,因此有
内,因此有 平面
平面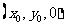 ,则
,则 ,因为
,因为 平面BOE,所以有
平面BOE,所以有 ,因此有
,因此有 ,即点M的坐标为
,即点M的坐标为 ,在平面直角坐标系
,在平面直角坐标系 中,
中, 的内部区域满足不等式组
的内部区域满足不等式组 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在 内存在一点
内存在一点 ,使
,使 ,
, 的距离为
的距离为 .
.  ;
;  的取值为
的取值为 的分布列为
的分布列为



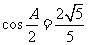 ,
, ,又由
,又由 ,得
,得
 ,
,
 ,又
,又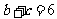 ,
, 或
或 ,由余弦定理得
,由余弦定理得 ,
,

 ,随着F点到C点时,因
,随着F点到C点时,因 平面
平面 ,即有
,即有 ,对于
,对于 ,又
,又 ,因此有
,因此有 ,则有
,则有 ,因此
,因此 的取值范围是
的取值范围是 种;若有一个台阶有2人,另一个是1人,则共有
种;若有一个台阶有2人,另一个是1人,则共有 种,因此共有不同的站法种数是336种.
种,因此共有不同的站法种数是336种. 
 ,二项指数分别为
,二项指数分别为 ,因此对于
,因此对于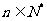 ,
,

 ;对于低峰部分为
;对于低峰部分为 ,二部分之和为
,二部分之和为