摘要:16. 某学生骑自行车上学途中要经过4个交叉路口.在各交叉路口遇到红灯的概率是(各交叉口遇到红灯的事件相互独立). (1) 求这名学生在上学途中3次遇到红灯的概率, (2) 求这名学生在途中最多遇到1次红灯的概率.
网址:http://m.1010jiajiao.com/timu_id_4465134[举报]
(09年湖南师大附中月考理)(13分)
某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元,每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管)。
(1)设该厂每![]() 天购买一次原材料,试写出每次购买的原材料在
天购买一次原材料,试写出每次购买的原材料在![]() 天内总的保管费用
天内总的保管费用![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(本小题满分13分)
某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?
查看习题详情和答案>>
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为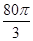 立方米,且
立方米,且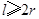 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为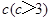 千元,设该容器的建造费用为
千元,设该容器的建造费用为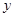 千元.
千元.
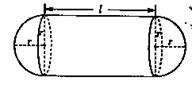
(Ⅰ)写出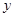 关于
关于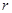 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的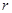 .
.
查看习题详情和答案>>
 各路口是否遇到红灯是相互独立的,遇到红灯的概率都是
各路口是否遇到红灯是相互独立的,遇到红灯的概率都是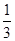 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.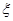 的分布列及期望.
的分布列及期望.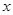 米。
米。