摘要：(一)创设情景.揭示课题 1.提出问题:一元二次方程 ax2+bx+c=0 (a≠0)的根与二次函数 y=ax2+bx+c(a≠0)的图象有什么关系? 2．先来观察几个具体的一元二次方程的根及其相应的二次函数的图象: ①方程与函数 ②方程与函数 ③方程与函数 1．师:引导学生解方程.画函数图象.分析方程的根与图象和轴交点坐标的关系.引出零点的概念． 生:独立思考完成解答.观察.思考.总结.概括得出结论.并进行交流． 师:上述结论推广到一般的一元二次方程和二次函数又怎样?
网址：http://m.1010jiajiao.com/timu_id_4460338[举报]
（1）求右焦点坐标是（2，0），且经过点（-2，-| 2 |
（2）已知椭圆C的方程是
| x2 |
| a2 |
| y2 |
| b2 |
（3）利用（2）所揭示的椭圆几何性质，用作图方法找出下面给定椭圆的中心，简要写出作图步骤，并在图中标出椭圆的中心． 查看习题详情和答案>>
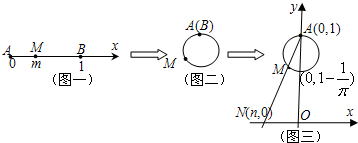如图揭示了一个由区间（0，1）到实数集R上的对应过程：区间（0，1）内的任意实数m与数轴上的线段AB（不包括端点）上的点M一一对应（图一），将线段AB围成一个圆，使两端A，B恰好重合（图二），再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1）（图三）．图三中直线AM与x轴交于点N（n，0），由此得到一个函数n=f（m），则下列命题中正确的序号是（ ）（1）f（
| 1 |
| 2 |
（2）f（x）是偶函数；
（3）f（x）在其定义域上是增函数；
（4）y=f（x）的图象关于点（
| 1 |
| 2 |
| A、（1）（3）（4） |
| B、（1）（2）（3） |
| C、（1）（2）（4） |
| D、（1）（2）（3）（4） |
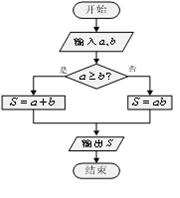
（2012•泉州模拟）定义一种运算S=a?b，在框图所表达的算法中揭示了这种运算“?”的含义．那么，按照运算“?”的含义，计算tan15°?tan30°+tan30°?tan15°=1
1
．
（I）已知椭圆C的方程是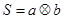
，在框图所表达的算法中揭示了这种运算“
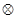”的含义.那么，按照运算“
．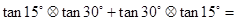