摘要：22．将图9中的电磁铁按下列要求连入你设计的电路中.要求:A．电路能改变电磁铁磁性的强弱,B．使小磁针静止时处于如图所示位置． 图8
网址：http://m.1010jiajiao.com/timu_id_4457651[举报]
已知△ABC和△ADE分别是以AB．AE为底的等腰直角三角形，以CE，CB为边作平行四边形CEHB，连DC，CH．
（1）如图1，当D点在AB上时，则∠DEH的度数为 ；CH与CD的数量关系是 ，并说明理由；
（2）将图1中的△ADE绕A点逆时针旋转45°得图2：则∠DEH的度数为 ，CH与CD之间的数量关系为 ；
（3）将图1中的△ADE绕A点顺时针旋转α（O°＜α＜45°）得图3，请探究CH与CD之间的数量关系，并给予证明．
查看习题详情和答案>>
（1）如图1，当D点在AB上时，则∠DEH的度数为
（2）将图1中的△ADE绕A点逆时针旋转45°得图2：则∠DEH的度数为
（3）将图1中的△ADE绕A点顺时针旋转α（O°＜α＜45°）得图3，请探究CH与CD之间的数量关系，并给予证明．
查看习题详情和答案>>
（2012•山西）问题情境：将一副直角三角板（Rt△ABC和Rt△DEF）按图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，试判断线段OM与ON的数量关系，并说明理由．
探究展示：小宇同学展示出如下正确的解法：
解：OM=ON，证明如下：
连接CO，则CO是AB边上中线，
∵CA=CB，∴CO是∠ACB的角平分线．（依据1）
∵OM⊥AC，ON⊥BC，∴OM=ON．（依据2）
反思交流：
（1）上述证明过程中的“依据1”和“依据2”分别是指：
依据1：
依据2：
（2）你有与小宇不同的思考方法吗？请写出你的证明过程．
拓展延伸：
（3）将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM、ON，试判断线段OM、ON的数量关系与位置关系，并写出证明过程．
查看习题详情和答案>>
探究展示：小宇同学展示出如下正确的解法：
解：OM=ON，证明如下：
连接CO，则CO是AB边上中线，
∵CA=CB，∴CO是∠ACB的角平分线．（依据1）
∵OM⊥AC，ON⊥BC，∴OM=ON．（依据2）
反思交流：
（1）上述证明过程中的“依据1”和“依据2”分别是指：
依据1：
等腰三角形的三线合一（等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合）
等腰三角形的三线合一（等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合）
依据2：
角平分线上的点到角的两边的距离相等
角平分线上的点到角的两边的距离相等
（2）你有与小宇不同的思考方法吗？请写出你的证明过程．
拓展延伸：
（3）将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM、ON，试判断线段OM、ON的数量关系与位置关系，并写出证明过程．
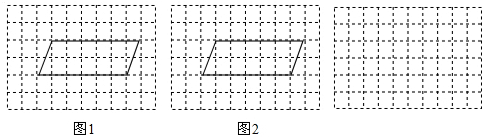
（2013•梅列区模拟）如图，正方形网格中的平行四边形的顶点都在格点上．
（1）请再图1中画一条直线把平行四边形分成面积相等的两部分；
（2）将图2中的平行四边形分割成四个全等四边形（在图②中画出分割线），并把所得的四个全等的四边形在图3中拼成一个轴对称图形或中心对称图形，使所得图形与原图形不全等且各个顶点都落在格点上．
查看习题详情和答案>>
（1）请再图1中画一条直线把平行四边形分成面积相等的两部分；
（2）将图2中的平行四边形分割成四个全等四边形（在图②中画出分割线），并把所得的四个全等的四边形在图3中拼成一个轴对称图形或中心对称图形，使所得图形与原图形不全等且各个顶点都落在格点上．
一次（若指针恰好指在分割线上，则重转一次，直到指针指向一个数字为止）．