摘要: 数列1.2.3.-.m.-前m项之和为5050.求值.
网址:http://m.1010jiajiao.com/timu_id_4453214[举报]
设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 在函数
在函数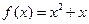 的图象上.
的图象上.
(1)求a1,a2,a3值,并求 的表达式;
的表达式;
(2)将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),(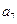 ,
,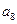 ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
,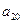 );(
);( ),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;w*w^w.k&s#5@u.c~o*m
的值;w*w^w.k&s#5@u.c~o*m
(3)设 为数列
为数列 的前
的前 项积,是否存在实数
项积,是否存在实数 ,使得不等式
,使得不等式 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知数列{an}是首项为1、公差为2的等差数列,对每一个k∈N*,在ak与ak+1之间插入2k-1个2,得到新数列{bn}.设Sn、Tn分别是数列{bn}和{an}的前n项和.
(1)试问a10是数列{bn}的第几项?
(2)是否存在正整数m,使Sm=2 008?若存在,求出m的值;若不存在,请说明理由.
(3)若am是数列{bn}的第f(m)项,试比较Sf(m)与2Tm的大小,并说明理由.
查看习题详情和答案>>已知定义在(-1,1)上的函数f(x)满足f![]() =1,且对x、y∈(-1,1)时,有f(x)-f(y)=
=1,且对x、y∈(-1,1)时,有f(x)-f(y)=![]() .
.
(1)判断f(x)在(-1,1)上的奇偶性,并证明之;
(2)令x1=![]() ,xn+1=
,xn+1=![]() ,求数列{f(xn)}的通项公式;
,求数列{f(xn)}的通项公式;
(3)设Tn为数列{![]() }的前n项和,问是否存在正整数m,使得对任意的n∈N*,有Tn<
}的前n项和,问是否存在正整数m,使得对任意的n∈N*,有Tn<![]() 成立?若存在,求出m的最小值;若不存在,则说明理由.
成立?若存在,求出m的最小值;若不存在,则说明理由.
有一个翻硬币游戏,开始时硬币正面朝上,然后掷骰子根据下列①、②、③的规则翻动硬币:①骰子出现1点时,不翻动硬币;②出现2,3,4,5点时,翻动一下硬币,使另一面朝上;③出现6点时,如果硬币正面朝上,则不翻动硬币;否则,翻动硬币,使正面朝上.按以上规则,在骰子掷了n次后,硬币仍然正面朝上的概率记为Pn.
(Ⅰ)求证:?n∈N*,点(Pn,Pn+1)恒在过定点( ,
, ),斜率为
),斜率为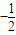 的直线上;
的直线上;
(Ⅱ)求数列{Pn}的通项公式Pn;
(Ⅲ)用记号Sn→m表示数列{ }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
查看习题详情和答案>>
(Ⅰ)求证:?n∈N*,点(Pn,Pn+1)恒在过定点(
 ,
, ),斜率为
),斜率为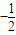 的直线上;
的直线上;(Ⅱ)求数列{Pn}的通项公式Pn;
(Ⅲ)用记号Sn→m表示数列{
 }从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.查看习题详情和答案>>
有一个翻硬币游戏,开始时硬币正面朝上,然后掷骰子根据下列①、②、③的规则翻动硬币:①骰子出现1点时,不翻动硬币;②出现2,3,4,5点时,翻动一下硬币,使另一面朝上;③出现6点时,如果硬币正面朝上,则不翻动硬币;否则,翻动硬币,使正面朝上.按以上规则,在骰子掷了n次后,硬币仍然正面朝上的概率记为Pn.
(Ⅰ)求证:?n∈N*,点(Pn,Pn+1)恒在过定点(
,
),斜率为-
的直线上;
(Ⅱ)求数列{Pn}的通项公式Pn;
(Ⅲ)用记号Sn→m表示数列{Pn-
}从第n项到第m项之和,那么对于任意给定的正整数k,求数列S1→k,Sk+1→2k,…,S(n-1)k+1→nk,…的前n项和Tn.
查看习题详情和答案>>
(Ⅰ)求证:?n∈N*,点(Pn,Pn+1)恒在过定点(
| 5 |
| 9 |
| 5 |
| 9 |
| 1 |
| 2 |
(Ⅱ)求数列{Pn}的通项公式Pn;
(Ⅲ)用记号Sn→m表示数列{Pn-
| 5 |
| 9 |