摘要:6.已知sin(a+b) =.sin(a-b) =.求的值 解:由题设: 从而 或设:x = ∵ ∴ ∴x = 即 =
网址:http://m.1010jiajiao.com/timu_id_4441900[举报]
已知函数f(x)=sin(ωx+φ),(ω>0,,0<φ<π)的一系列对应值如表:
(Ⅰ)求f(x)的解析式;
(Ⅱ)在△ABC中,a、b、c分别是△ABC的对边,若f(A)=
,c=2,a=
b,求△ABC的面积.
查看习题详情和答案>>
| x | -
|
|
|
|
| ||||||||||
| y | 0 | 1 | 0 | -1 | 0 |
(Ⅱ)在△ABC中,a、b、c分别是△ABC的对边,若f(A)=
| 1 |
| 2 |
| 3 |
已知角a的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3,
).
(1)定义行列式
=a•d-b•c,解关于x的方程:
+1=0;
(2)若函数f(x)=sin(x+a)+cos(x+a)(x∈R)的图象关于直线x=x0对称,求tanx0的值. 查看习题详情和答案>>
| 3 |
(1)定义行列式
|
|
(2)若函数f(x)=sin(x+a)+cos(x+a)(x∈R)的图象关于直线x=x0对称,求tanx0的值. 查看习题详情和答案>>
已知二阶矩阵M=(
)有特征值λ1=2及对应的一个特征向量
1=
.
(Ⅰ)求矩阵M;
(II)若
=
,求M10
.
(2)已知直线l:
(t为参数),曲线C1:
(θ为参数).
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的
倍,纵坐标压缩为原来的
倍,得到曲线C2C,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
(3)已知函数f(x)=log2(|x+1|+|x-2|-m).
(Ⅰ)当m=5时,求函数f(x)的定义域;
(Ⅱ)若关于x的不等式f(x)≥1的解集是R,求m的取值范围.
查看习题详情和答案>>
|
| e |
|
(Ⅰ)求矩阵M;
(II)若
| a |
|
| a |
(2)已知直线l:
|
|
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的
| 1 |
| 2 |
| ||
| 2 |
(3)已知函数f(x)=log2(|x+1|+|x-2|-m).
(Ⅰ)当m=5时,求函数f(x)的定义域;
(Ⅱ)若关于x的不等式f(x)≥1的解集是R,求m的取值范围.
已知向量
=(sinωx,2cosωx),
=(cosωx,-
cosωx)(ω>0),函数f(x)=
(
+
)-1,且函数f(x)的最小正周期为
.
(1)求ω的值;
(2)设△ABC的三边a、b、c满足:b2=ac,且边b所对的角为x,若方程f(x)=k有两个不同的实数解,求实数k的取值范围.
查看习题详情和答案>>
| a |
| b |
2
| ||
| 3 |
| a |
| 3 |
| b |
| a |
| π |
| 2 |
(1)求ω的值;
(2)设△ABC的三边a、b、c满足:b2=ac,且边b所对的角为x,若方程f(x)=k有两个不同的实数解,求实数k的取值范围.
已知函数f(x)=sin(ωx+φ),(ω>0,,0<φ<π)的一系列对应值如表:
| x | 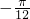 |  |  |  |  |
| y | 0 | 1 | 0 | -1 | 0 |
(Ⅱ)在△ABC中,a、b、c分别是△ABC的对边,若
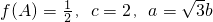 ,求△ABC的面积.
查看习题详情和答案>>
,求△ABC的面积.
查看习题详情和答案>>