网址:http://m.1010jiajiao.com/timu_id_4440501[举报]
解:(1)点C的坐标为![]() .
.
∵ 点A、B的坐标分别为![]() ,
,
∴ 可设过A、B、C三点的抛物线的解析式为![]() .
.
将![]() 代入抛物线的解析式,得
代入抛物线的解析式,得![]() .
.
∴ 过A、B、C三点的抛物线的解析式为![]() .
.
 (2)可得抛物线的对称轴为
(2)可得抛物线的对称轴为![]() ,顶点D的坐标为
,顶点D的坐标为
![]() ,设抛物线的对称轴与x轴的交点为G.
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为![]() .
.
设点P的坐标为![]() .
.
解法一:如图8,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ![]() ,即
,即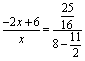 .
.
解得![]() . 经检验
. 经检验![]() 是原方程的解.
是原方程的解.
此时点P的坐标为![]() .
.
但此时![]() ,OM<GA.
,OM<GA.
∵ ![]()
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P. - - - - - - - - - - - - - - - - - - - - - 6分
解法二:如图9,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于
点N. 则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由![]() ,可得E点的坐标为
,可得E点的坐标为![]() .
.
NE=EG=![]() , ON=OE-NE=
, ON=OE-NE=![]() ,NP=DG=
,NP=DG=![]() .
.
∴ 点P的坐标为![]() .∵ x=
.∵ x=![]() 时,
时,![]() ,
,
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P .

(3)![]() 的取值范围是
的取值范围是![]() .
.
解密码:
下面的六道题算式真是莫名其妙,但当你知道这是密码算式每个数字各自对应的是另一个不同数字时,事情就讲得通了,请你设法填出表中密码所对应的原来数字.
(1)8+7=62;(2)5+3=5;(3)12+8=23;(4)50+9=54;(5)11×1=55;(6)0-9=1

代数式(π-1)x2y3z是多项式,还是单项式?若是多项式,指出其项数和次数;若是单项式,指出其系数和次数.下面是小明和小华的解答.
小明:因为(π-1)x2y3z可以写成πx2y3z-x2y3z,所以它是多项式,它是一个七次二项式.
小华:(π-1)x2y3z是一个单项式,(π-1)是它的系数,次数是6.
你认为谁的解答是错误的?错误的原因是什么?
已知:抛物线C1 :![]() 经过点A(-1,0)、B (3,0)、C(0,-3).
经过点A(-1,0)、B (3,0)、C(0,-3).
(1)求抛物线C1的解析式;
(2)将抛物线C1向左平移几个单位长度,可使所得的抛物线C2经过坐标原点,并写出C2的解析式;
| |