摘要:教法:以问题为载体.有引导的对话.让学生经历知识的形成过程和发展过程.从而突出教学重点.并采用多媒体教学.增加课堂容量.有利于学生活动的充分展开.
网址:http://m.1010jiajiao.com/timu_id_4439920[举报]
(2009•上海模拟)已知点列B1(1,y1),B2(2,y2),…,Bn(n,yn),…(n∈N*)顺次为直线y=
上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.
(1)证明:数列{yn}是等差数列;
(2)求证:对任意的n∈N*,xn+2-xn是常数,并求数列{xn}的通项公式;
(3)对上述等腰三角形AnBnAn+1添加适当条件,提出一个问题,并做出解答.(根据所提问题及解答的完整程度,分档次给分)
查看习题详情和答案>>
| x | 4 |
(1)证明:数列{yn}是等差数列;
(2)求证:对任意的n∈N*,xn+2-xn是常数,并求数列{xn}的通项公式;
(3)对上述等腰三角形AnBnAn+1添加适当条件,提出一个问题,并做出解答.(根据所提问题及解答的完整程度,分档次给分)
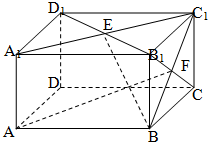 如图,在长方体AC1中,AB=BC=2,AA1=
如图,在长方体AC1中,AB=BC=2,AA1=| 2 |
(1)求异面直线AF和BE所成的角;
(2)求直线AF和平面BEC所成角的正弦值.
 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,
|
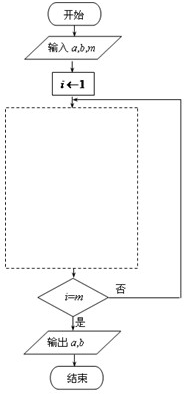
(1)可考虑利用算法来求am,bm的值,其中m为给定的数据(m≥2,m∈N).右图算法中,虚线框中所缺的流程,可以为下面A、B、C、D中的
ACD
ACD
(请填出全部答案)
A、
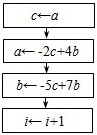 B、
B、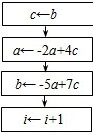
C、
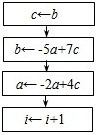 D、
D、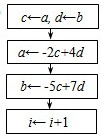
(2)我们可证明当a≠b,5a≠4b时,{an-bn}及{5an-4bn}均为等比数列,请按答纸题要求,完成一个问题证明,并填空.
证明:{an-bn}是等比数列,过程如下:an-bn=(-2an-1+4bn-1)+(5an-1-7bn-1)=3an-1-3bn-1=3(an-1-bn-1)
所以{an-bn}是以a1-b1=a-b≠0为首项,以
3
3
为公比的等比数列;同理{5an-4bn}是以5a1-4b1=5a-4b≠0为首项,以
2
2
为公比的等比数列(3)若将an,bn写成列向量形式,则存在矩阵A,使
|
|
|
|
|
①写出矩阵A=
|
|
P=
,Q=
|
|
P=
,Q=
; ③矩阵Cn中的唯一元素是
|
|
2n+2-4
2n+2-4
.计算过程如下: