摘要：3．线性回归 回归分析:对于两个变量.当自变量取值一定时.因变量的取值带有一定随机性的两个变量之间的关系叫相关关系或回归关系. 回归直线方程:设x与y是具有相关关系的两个变量.且相应于n个观测值的n个点大致分布在某一条直线的附近.就可以认为y对x的回归函数的类型为直线型:.其中..我们称这个方程为y对x的回归直线方程.
网址：http://m.1010jiajiao.com/timu_id_4439731[举报]
对于两个变量
和
进行回归分析，得到一组样本数据：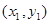
，
，…，
，下列说法中错误的是
A.由样本数据得到的回归方程
必过样本中心点
B.残差的平方和越小的模型，拟合的效果越好
C.用
来刻画回归效果，越小，说明拟合效果越好
D.若样本点呈条状分布，则变量和之间具有比较好的线性相关关系
查看习题详情和答案>>
对两个变量y和x进行回归分析，得到一组样本数据：(x1，y1)，(x2，y2)…，(xn，yn)，计算线性相关系数γ；并由样本数据得到回归方程y＝bx＝a再计算残差平方和与相关指数R2．
①线性回归方程y＝bx＝a必过样本中心(
；
②线性相关系数γ的绝对值越接近于1，表明两个随机变量线性相关性越强；
③用相关指数R2来刻画回归效果，R2越小，说明模型的拟合效果越好；
④在回归分析中，残差平方和代表了数据点和它在回归直线上相应位置的差异．
则以上说法正确的是________．(写出所有正确说法的序号)
某种产品的年销售量y和该年广告费用支出x有关，现收集了5组观测数据列于下表：
现确定以广告费用支出x为解释变量，销售量y为预报变量对这两个变量进行统计分析．
参考公式：
=
=
，
=
-
，R2=1-
=
xi，
=
yi
（Ⅰ）作y和x的散点图，根据该图猜想它们之间是什么相关关系．
（Ⅱ）如果是线性相关关系，请用给出的最小二乘法公式求回归直线方程；否则说明它们之间更趋近于什么非线性相关关系．
（Ⅲ）假如2011年广告费用支出为10万元，请根据你得到的模型，预报该年的销售量y，并用R2的值说明解释变量对于预报变量变化的贡献率． 查看习题详情和答案>>
| x/万元 | 2 | 4 | 5 | 6 | 8 | 参考数据：
| |||||||||||||
| y/万件 | 30 | 40 | 60 | 50 | 70 |
参考公式：
| ? |
| b |
| |||||||
|
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
| |||||
|
. |
| x |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| y |
| 1 |
| n |
| n |
|
| i=1 |
（Ⅰ）作y和x的散点图，根据该图猜想它们之间是什么相关关系．
（Ⅱ）如果是线性相关关系，请用给出的最小二乘法公式求回归直线方程；否则说明它们之间更趋近于什么非线性相关关系．
（Ⅲ）假如2011年广告费用支出为10万元，请根据你得到的模型，预报该年的销售量y，并用R2的值说明解释变量对于预报变量变化的贡献率． 查看习题详情和答案>>