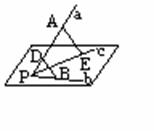
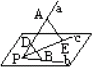
摘要：(1)证明:设=a.=b.=c.则|a|=|b|.∵=b-a. ∴·=(b-a)·c=b·c-a·c=|b|·|c|cos60°-|a|·|c|cos60°=0. ∴C1C⊥BD. (2)解:连AC.BD.设AC∩BD=O.连OC1.则∠C1OC为二面角α-BD-β的平面角. ∵(a+b).(a+b)-c ∴·(a+b)·［(a+b)-c］ =(a2+2a·b+b2)-a·c-b·c =-·2·cos60°-·2·cos60°=. 则||=.||=.∴cosC1OC= (3)解:设=x.CD=2. 则CC1=. ∵BD⊥平面AA1C1C.∴BD⊥A1C ∴只须求满足:=0即可. 设=a.=b.=c. ∵=a+b+c.=a-c. ∴=(a+b+c)(a-c)=a2+a·b-b·c-c2=-6.令6-=0.得x=1或x=-. 评述:本题蕴涵着转化思想.即用向量这个工具来研究空间垂直关系的判定.二面角的求解以及待定值的探求等问题.

网址：http://m.1010jiajiao.com/timu_id_4435245[举报]