摘要:19.(Ⅰ)证明:连接. 在中.分别是的中点.所以. 又.所以.又平面ACD .DC平面ACD. 所以平面ACD (Ⅱ)在中..所以 而DC平面ABC..所以平面ABC 而平面ABE. 所以平面ABE平面ABC. 所以平面ABE 由(Ⅰ)知四边形DCQP是平行四边形.所以 所以平面ABE. 所以直线AD在平面ABE内的射影是AP. 所以直线AD与平面ABE所成角是 在中. . 所以 20090423 20.设为数列的前项和...其中是常数. (I) 求及, (II)若对于任意的...成等比数列.求的值.
网址:http://m.1010jiajiao.com/timu_id_4431435[举报]
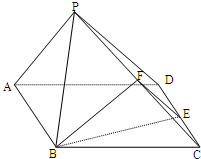 16、如图,在四棱锥P-ABCD中,四边形ABCD为菱形,∠BCD=60°,△PAB为正三角形,点E,F分别是CD、CP的中点,连接BE、BF、EF.
16、如图,在四棱锥P-ABCD中,四边形ABCD为菱形,∠BCD=60°,△PAB为正三角形,点E,F分别是CD、CP的中点,连接BE、BF、EF.(1)求证:AB⊥PD;
(2)求证:平面BEF⊥平面ABCD;
(3)问:在BE上是否存在点G,使得FG∥平面PAB,并说明理由.
如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)设PD=AD=a, 求三棱锥B-EFC的体积.

【解析】第一问利用线面平行的判定定理, ,得到
,得到
第二问中,利用
 ,所以
,所以
又因为 ,
, ,从而得
,从而得
第三问中,借助于等体积法来求解三棱锥B-EFC的体积.
(Ⅰ)证明:
 分别是
分别是 的中点,
的中点, 
 ,
, . …4分
. …4分
(Ⅱ)证明: 四边形
四边形 为正方形,
为正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴

查看习题详情和答案>>
如图1,在直角梯形 中,
中,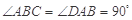 ,
,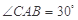 ,
,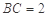 ,
,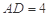 . 把
. 把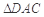 沿对角线
沿对角线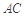 折起到
折起到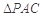 的位置,如图2所示,使得点
的位置,如图2所示,使得点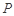 在平面
在平面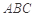 上的正投影
上的正投影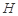 恰好落在线段
恰好落在线段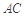 上,连接
上,连接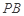 ,点
,点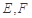 分别为线段
分别为线段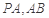 的中点.
的中点.
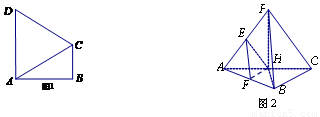
(1)求证:平面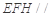 平面
平面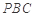 ;
;
(2)求直线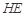 与平面
与平面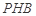 所成角的正弦值;
所成角的正弦值;
(3)在棱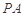 上是否存在一点
上是否存在一点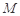 ,使得
,使得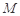 到点
到点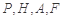 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.
查看习题详情和答案>>
 中,
中, ,
, ,
,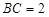 ,
,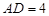 . 把
. 把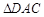 沿对角线
沿对角线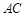 折起到
折起到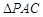 的位置,如图2所示,使得点
的位置,如图2所示,使得点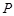 在平面
在平面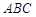 上的正投影
上的正投影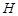 恰好落在线段
恰好落在线段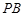 ,点
,点 分别为线段
分别为线段 的中点.
的中点. 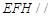 平面
平面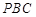 ;
;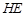 与平面
与平面 所成角的正弦值;
所成角的正弦值;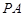 上是否存在一点
上是否存在一点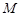 ,使得
,使得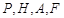 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.
 中,
中,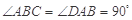 ,
, ,
,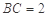 ,
,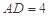 . 把
. 把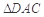 沿对角线
沿对角线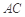 折起到
折起到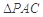 的位置,如图2所示,使得点
的位置,如图2所示,使得点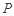 在平面
在平面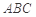 上的正投影
上的正投影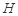 恰好落在线段
恰好落在线段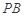 ,点
,点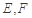 分别为线段
分别为线段 的中点.
的中点. 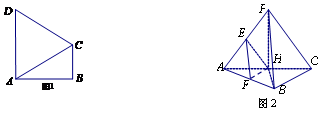
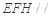 平面
平面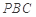 ;
;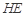 与平面
与平面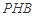 所成角的正弦值;
所成角的正弦值;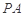 上是否存在一点
上是否存在一点 ,使得
,使得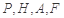 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.