题目内容
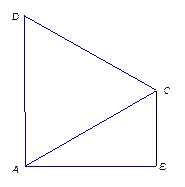
如图1,在直角梯形 中,
中,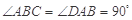 ,
,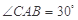 ,
,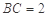 ,
,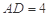 . 把
. 把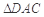 沿对角线
沿对角线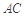 折起到
折起到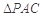 的位置,如图2所示,使得点
的位置,如图2所示,使得点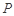 在平面
在平面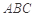 上的正投影
上的正投影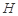 恰好落在线段
恰好落在线段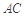 上,连接
上,连接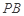 ,点
,点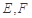 分别为线段
分别为线段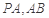 的中点.
的中点.
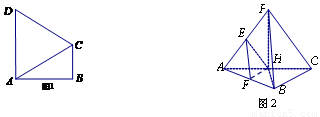
(1)求证:平面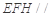 平面
平面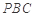 ;
;
(2)求直线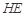 与平面
与平面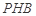 所成角的正弦值;
所成角的正弦值;
(3)在棱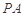 上是否存在一点
上是否存在一点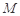 ,使得
,使得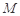 到点
到点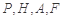 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.
(1)证明过程详见解析;(2)正弦值为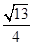 ;(3)存在,点E即为所求.
;(3)存在,点E即为所求.
【解析】
试题分析:本题以三棱锥为几何背景考查面面平行和二面角的求法,可以运用传统几何法,也可以用空间向量法求解,突出考查空间想象能力和计算能力.第一问,首先由点 的正投影
的正投影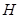 在
在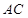 上得
上得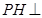 平面
平面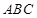 ,利用线面垂直的性质,得
,利用线面垂直的性质,得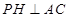 ,在原直角梯形中,利用已知的边和角,得到
,在原直角梯形中,利用已知的边和角,得到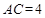 ,
,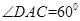 ,所以得到
,所以得到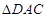 为等边三角形,从而知
为等边三角形,从而知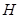 是
是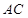 的中点,所以可得
的中点,所以可得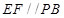 ,
,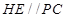 ,
,
利用面面平行的判定得出证明;第二问,先建立空间直角坐标系,写出所需点的坐标,先设出平面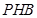 的法向量
的法向量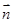 ,利用
,利用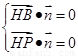 求出
求出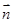 ,利用夹角公式求直线
,利用夹角公式求直线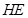 和法向量
和法向量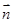 所在直线的夹角;第三问,由已知和前2问过程中得到的数据,可以看出
所在直线的夹角;第三问,由已知和前2问过程中得到的数据,可以看出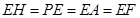 ,所以
,所以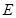 点即为所求.
点即为所求.
试题解析:(I)因为点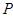 在平面
在平面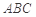 上的正投影
上的正投影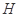 恰好落在线段
恰好落在线段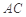 上,
上,
所以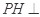 平面
平面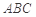 ,所以
,所以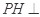
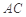 ,
1分
,
1分
因为在直角梯形 中,
中,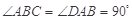 ,
,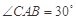 ,
,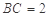 ,
,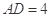 ,
,
所以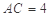 ,
,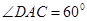 ,所以
,所以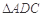 是等边三角形,
是等边三角形,
所以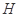 是
是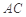 中点,
2分
中点,
2分
所以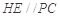 ,
3分
,
3分
同理可证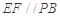 ,
,
又 ,
,
所以平面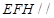 平面
平面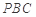 .
5分
.
5分
(II)在平面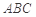 内过
内过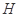 作
作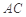 的垂线 如图建立空间直角坐标系,则
的垂线 如图建立空间直角坐标系,则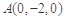 ,
,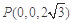 ,
,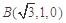 ,
6分
,
6分
因为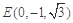 ,
,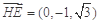 ,
,
设平面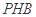 的法向量为
的法向量为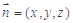 ,
,
因为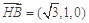 ,
,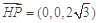 ,
,
所以有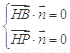 ,即
,即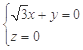 ,
,
令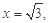 则
则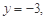 所以
所以 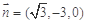 ,
8分
,
8分
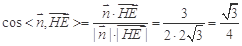 ,
10分
,
10分
所以直线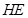 与平面
与平面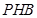 所成角的正弦值为
所成角的正弦值为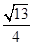 .
11分
.
11分
(III)存在,事实上记点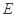 为
为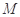 即可
12分
即可
12分
因为在直角三角形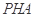 中,
中,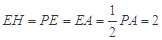 , 13分
, 13分
在直角三角形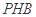 中,点
中,点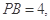
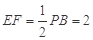 ,
,
所以点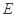 到四个点
到四个点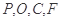 的距离相等.
14分
的距离相等.
14分
考点:1.线面垂直的判定;2.中位线的性质;3.面面平行的判定;4.线面角的求法;5.夹角公式;6.向量法.

 中,
中, ,
, ,
,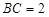 ,
,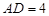 . 把
. 把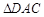 沿对角线
沿对角线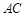 折起到
折起到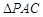 的位置,如图2所示,使得点
的位置,如图2所示,使得点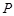 在平面
在平面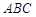 上的正投影
上的正投影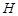 恰好落在线段
恰好落在线段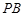 ,点
,点 分别为线段
分别为线段 的中点.
的中点. 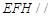 平面
平面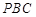 ;
;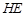 与平面
与平面 所成角的正弦值;
所成角的正弦值;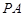 上是否存在一点
上是否存在一点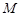 ,使得
,使得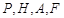 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.
 中,
中,  ,
,  ,
, ,
, 为线段
为线段 的中点. 将
的中点. 将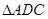 沿
沿 折起,使平面
折起,使平面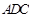
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示. 平面
平面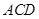 ;
;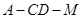 的余弦值.
的余弦值. 
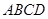 中,
中,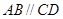 ,
, ,且
,且 .
.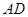 为一边向形外作正方形
为一边向形外作正方形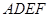 ,然后沿边
,然后沿边 为
为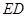 的中点,如图2.
的中点,如图2.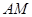 ∥平面
∥平面 ;
;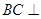 平面
平面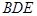 ;
;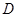 到平面
到平面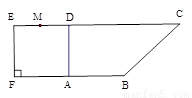

 图
图
 中,
中,  ,
,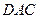 沿对角线
沿对角线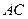 折起后如图2所示(点
折起后如图2所示(点 记为点
记为点 ), 点
), 点 上的正投影
上的正投影 落在线段
落在线段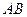 上, 连接
上, 连接 .
. 与平面
与平面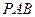 所成的角的大小;
所成的角的大小; 的大小的余弦值.
的大小的余弦值.