摘要：非等比数列中.前n项和. (1)求数列的通项公式, (2)设..是否存在最大的整数m.使得对任意的n 均有总成立?若存在.求出m,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu_id_4429812[举报]
数列{an}的前n项和记为Sn，前kn项和记为Skn（n，k∈N*），对给定的常数k，若
是与n无关的非零常数t=f（k），则称该数列{an}是“k类和科比数列”．
（1）已知Sn=
an-
(n∈N*)，求数列{an}的通项公式；
（2）在（1）的条件下，数列an=2cn，求证数列cn是一个“1 类和科比数列”（4分）；
（3）设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1与D的数量关系，并写出相应的常数t=f（k）． 查看习题详情和答案>>
| S(k+1)n |
| Skn |
（1）已知Sn=
| 4 |
| 3 |
| 2 |
| 3 |
（2）在（1）的条件下，数列an=2cn，求证数列cn是一个“1 类和科比数列”（4分）；
（3）设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1与D的数量关系，并写出相应的常数t=f（k）． 查看习题详情和答案>>
数列{an}的前n项和记为Sn，前kn项和记为Skn（n，k∈N*），对给定的常数k，若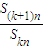
是与n无关的非零常数t=f（k），则称该数列{an}是“k类和科比数列”．
（1）已知
，求数列{an}的通项公式；
（2）在（1）的条件下，数列
，求证数列cn是一个“1 类和科比数列”（4分）；
（3）设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1与D的数量关系，并写出相应的常数t=f（k）．
查看习题详情和答案>>
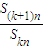是与n无关的非零常数t=f（k），则称该数列{an}是“k类和科比数列”．（1）已知
，求数列{an}的通项公式；（2）在（1）的条件下，数列
，求证数列cn是一个“1 类和科比数列”（4分）；（3）设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1与D的数量关系，并写出相应的常数t=f（k）．
查看习题详情和答案>>
数列{an}的前n项和记为Sn，前kn项和记为
Skn(n，k∈N*)，对给定的常数k，若
是与n无关的非零常数t＝f(k)，则称该数列{an}是“k类和科比数列”，
(1)已知Sn＝
an－
(n∈N*)，求数列{an}的通项公式；
(2)在(1)的条件下，数列an＝2cn，求证数列{cn}是一个“1类和科比数列”；
(3)、设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1
与D的数量关系，并写出相应的常数t＝f(k)；
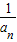}的前n项和为Sn，求证：
．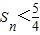