摘要：例1:(1)设是定义域为R的任一函数. . ①判断与的奇偶性, ②试将函数表示为一个奇函数与一个偶函数的和 例2:定义在实数集上的函数.对任意.有且. (1) 求证: (2)判断的奇偶性 (3)若存在正数C.使.①求证对任意.有成立 ②试问函数是不是周期函数.如果是.找出它的一个周期,如果不是请证明. 例3:已知函数 (1) 求的解析式和定义域 (2) 设的反函数是.求证:当时.成立 例4:已知奇函数的定义域为R.且在上增函数.当时.是否存在这样的实数.使对所有均成立?若存在.求所有适合条件的实数.若存在.说明理由.
网址：http://m.1010jiajiao.com/timu_id_4429629[举报]
设函数f(x)的定义域为R，若存在常数M>0，使得|f(x)|≤M|x|对一切实数x均成立，则称f(x)为F函数，给出下列函数：
①f(x)=0；
②f(x)=x2；
③f(x)=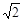
(sinx+cosx)；
④f(x)=
；
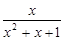⑤f(x)是定义在R上的奇函数，且对于任意实数x1，x2，均有|f(x1)－f(x2)|≤2|x1－x2|。
则其中是F函数的序号是___________________
查看习题详情和答案>>
设函数f(x)的定义域为R，若存在常数M>0，使得|f(x)|≤M|x|对一切实数x均成立，则称f(x)为F函数，给出下列函数：
①f(x)=0； ②f(x)=x2； ③f(x)=
(sinx+cosx)； ④f(x)=
；
⑤f(x)是定义在R上的奇函数，且对于任意实数x1，x2，均有|f(x1)－f(x2)|≤2|x1－x2|。
则其中是F函数的序号是___________________
设函数f(x)的定义域为R，若存在常数M>0，使得|f(x)|≤M|x|对一切实数x均成立，则称f(x)为F函数，给出下列函数：
①f(x)=0； ②f(x)=x2； ③f(x)=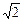
(sinx+cosx)； ④f(x)=
；
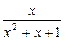⑤f(x)是定义在R上的奇函数，且对于任意实数x1，x2，均有|f(x1)－f(x2)|≤2|x1－x2|。
则其中是F函数的序号是___________________
①f(x)=0； ②f(x)=x2； ③f(x)=
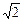(sinx+cosx)； ④f(x)=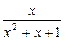；⑤f(x)是定义在R上的奇函数，且对于任意实数x1，x2，均有|f(x1)－f(x2)|≤2|x1－x2|。
则其中是F函数的序号是___________________
| |||||||||||||||
(n∈N*)。
对一切n∈N*均成立，若存在，求出k的最大值，并证明，否则说明理由。