摘要：解:过C作AB的垂线.交直线AB于点D.得到Rt△ACD与Rt△BCD． 设BD＝x海里. 在Rt△BCD中.tan∠CBD＝. ∴CD＝x ·tan63.5°． 在Rt△ACD中.AD＝AB+BD＝海里.tanA＝. ∴CD＝ ·tan21.3°． ∴x·tan63.5°＝·tan21.3°.即 ． 解得.x＝15． 答:轮船继续向东航行15海里.距离小岛C最近
网址：http://m.1010jiajiao.com/timu_id_4405920[举报]
如图，一直线与反比例函数y=
（k＞0）交于A、B两点，直线与x轴，y轴分别交于C，D两点，过A，B两点分别向x轴，y轴作垂线，H、E、F、I为垂足，BF与AE交于G点．
（1）矩形OFBI与矩形OHAE的面积和为______；（用含七的代数式表示）；
（2）求证：①AG•GF=EG•GB；②AC=BD；
（3）若直线AB的解析式为y=2x+2，且AB=2CD，反比例函数解析式为______．
查看习题详情和答案>>
如图，直线y=x+b（b＜0）交坐标轴于A、B两点，交双曲线y=
于点D，过D作两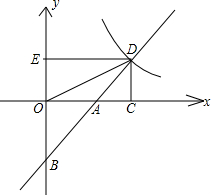
坐标轴的垂线DC、DE，连接OD．
（1）求证：DA平分∠CDE．
（2）是否存在直线AB．使得四边形OBCD为平行四边形？若存在，求出直线的解析式；若不存在，请说明理由．
（3）当△AOD的面积为3时，求直线AB的解析式． 查看习题详情和答案>>
| 8 | x |
坐标轴的垂线DC、DE，连接OD．（1）求证：DA平分∠CDE．
（2）是否存在直线AB．使得四边形OBCD为平行四边形？若存在，求出直线的解析式；若不存在，请说明理由．
（3）当△AOD的面积为3时，求直线AB的解析式． 查看习题详情和答案>>
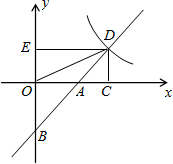如图，直线y=x+b（b≠0）交坐标轴于A、B两点，交双曲线y=| 2 | x |
（1）求证：AD平分∠CDE；
（2）对任意的实数b（b≠0），求证：AD•BD为定值；
（3）是否存在直线AB，使得四边形OBCD为平行四边形？若存在，求出直线的解析式；若不存在，请说明理由． 查看习题详情和答案>>
如图，在直角坐标系中，抛物线与坐标轴分别交于A（0，3），B（
如图，直线y=x+b（b≠0）交坐标轴于A、B两点，交双曲线y=