摘要:解:(1)当时.由得. ,(且)------------------------------------------------------2分 当时.由.得--------------------------------------4分 ∴---------------------------5分 (2)当且时.由<0,解得.---------------6分 当时.------------------------------8分 ∴函数的单调减区间为---------------------------------------9分 (3)对.都有即.也就是对恒成立.-------------------------------------------11分 由(2)知当时. ∴函数在和都单调递增-----------------------------------------------12分 又. 当时.∴当时. 同理可得.当时.有. 综上所述得.对. 取得最大值2, ∴实数的取值范围为.----------------------------------------------------------------14分 11(1)解:函数有一个零点为5.即方程.有一个根为5.将代入方程得.∴.∴---------------1分 由得 ∴或-------------------------------3分 由(1)知.∴不合舍去 由得---------------------------4分 方法1:由得----------------------5分 ∴数列是首项为.公比为的等比数列 ∴.∴-------------------------------6分 (方法2:由---①得当时----② ①-②得 ∴()即数列是首项为.公比为的等比数列 ∵.∴---------------③ 由①得代入③整理得) 知 ∴=------8分 ∵对有.∴ ∴.即---------------------------------------------10分 (3)由得 ∴=-----------------------11分 令.则.= ∵函数在上为增函数.在上为减函数-----12分 当时.当时.当时..当时. ∵.且 ∴当时,有最小值.即数列有最小项.最小项为 --------------------------------------------------------13分 当即时.有最大值.即数列有最大项.最大项为.
网址:http://m.1010jiajiao.com/timu_id_4398263[举报]
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形![]() 中,已知过点
中,已知过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() 。若
。若![]() 。
。
(1)求证:![]() 与
与![]() 的关系为
的关系为![]() ;
;
(2)设![]() ,定义函数
,定义函数![]() ,点列
,点列![]() 在函数
在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以首项为1,公比为
是以首项为1,公比为![]() 的等比数列,
的等比数列,![]() 为原点,令
为原点,令![]() ,是否存在点
,是否存在点![]()
![]() ,使得
,使得![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数![]() 为
为![]() 上偶函数,当
上偶函数,当![]() 时
时![]() ,又函数
,又函数![]() 图象关于直线
图象关于直线![]() 对称, 当方程
对称, 当方程![]() 在
在![]() 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数![]() 的取值范围。
的取值范围。
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。
(1)求证: 与
与 的关系为
的关系为 ;
;
(2)设 ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数 为
为 上偶函数,当
上偶函数,当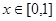 时
时 ,又函数
,又函数 图象关于直线
图象关于直线 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。
查看习题详情和答案>>
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形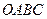 中,已知过点
中,已知过点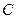 的直线与线段
的直线与线段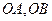 分别相交于点
分别相交于点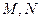 。若
。若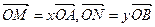 。
。
(1)求证: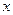 与
与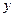 的关系为
的关系为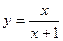 ;
;
(2)设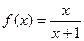 ,定义函数
,定义函数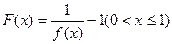 ,点列
,点列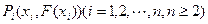 在函数
在函数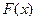 的图像上,且数列
的图像上,且数列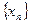 是以首项为1,公比为
是以首项为1,公比为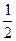 的等比数列,
的等比数列,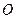 为原点,令
为原点,令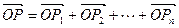 ,是否存在点
,是否存在点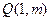
 ,使得
,使得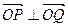 ?若存在,请求出
?若存在,请求出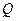 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数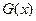 为
为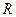 上偶函数,当
上偶函数,当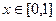 时
时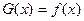 ,又函数
,又函数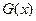 图象关于直线
图象关于直线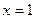 对称,当方程
对称,当方程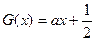 在
在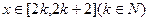 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数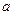 的取值范围。
的取值范围。
在平行四边形
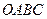 中,已知过点
中,已知过点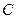 的直线与线段
的直线与线段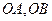 分别相交于点
分别相交于点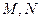 。若
。若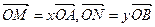 。
。(1)求证:
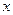 与
与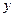 的关系为
的关系为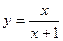 ;
;(2)设
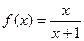 ,定义函数
,定义函数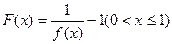 ,点列
,点列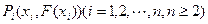 在函数
在函数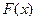 的图像上,且数列
的图像上,且数列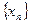 是以首项为1,公比为
是以首项为1,公比为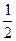 的等比数列,
的等比数列,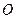 为原点,令
为原点,令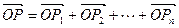 ,是否存在点
,是否存在点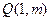
 ,使得
,使得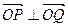 ?若存在,请求出
?若存在,请求出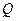 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。(3)设函数
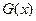 为
为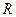 上偶函数,当
上偶函数,当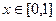 时
时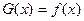 ,又函数
,又函数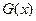 图象关于直线
图象关于直线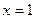 对称,当方程
对称,当方程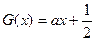 在
在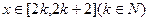 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数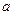 的取值范围。
的取值范围。 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。 与
与 的关系为
的关系为 ;
; ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。 为
为 上偶函数,当
上偶函数,当 时
时 ,又函数
,又函数 对称,当方程
对称,当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。 对任意的实数
对任意的实数 ,都有
,都有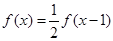 ,且当
,且当 时,
时, 。
。 时,求
时,求 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点 ,使得函数在点
,使得函数在点 平行。若存在,那么这样的点
平行。若存在,那么这样的点 ,且
,且  ,记
,记 ,求证:
,求证:  。
。