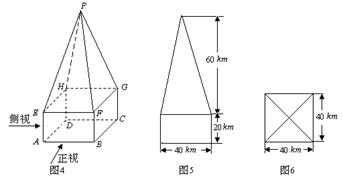
摘要：如图所示,在矩形ABCD中.AD=2AB=2.点E是AD的中点.将△DEC沿CE折起到△D′EC的位置.使二面角D′-EC-B是直二面角. (1)证明:BE⊥C D′, (2)求二面角D′-BC-E的正切值. 4如图:直三棱柱ABC-A1B1C1中. AC=BC=AA1=2.∠ACB=90°.E为BB1的中点.D点在AB上且DE=. (Ⅰ)求证:CD⊥平面A1ABB1, (Ⅱ)求三棱锥A1-CDE的体积.
网址：http://m.1010jiajiao.com/timu_id_4398126[举报]
中，
，
，
．
平面
；
的余弦值．
（09年湖南十二校理）我们知道，平面几何中有些正确的结论在空间中不一定成立.下面给出的平面几何中的四个真命题：
①平行于同一条直线的两条直线必平行；
②垂直于同一条直线的两条直线必平行;
③一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补；
④一个角的两边分别垂直于另一个角的两边，那么这两个角相等或互补.
在空间中仍然成立的有 ( )
A. ②③ B. ①④ C. ②④ D.①③ 查看习题详情和答案>>
高三第一学期期末四校联考数学第I卷中共有8道选择题，每道选择题有4个选项，其中只有一个是正确的；评分标准规定：“每题只选一项，答对得5分，不答或答错得0分．”某考生每道题都给出一个答案，已确定有5道题的答案是正确的，而其余选择题中，有1道题可判断出两个选项是错误的，有一道可以判断出一个选项是错误的，还有一道因不了解题意只能乱猜，试求出该考生：
（1）得40分的概率；
（2）得多少分的可能性最大？
（3）所得分数ξ的数学期望． 查看习题详情和答案>>
（1）得40分的概率；
（2）得多少分的可能性最大？
（3）所得分数ξ的数学期望． 查看习题详情和答案>>
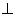平面PEG
中，
平面
，底面
.
时，求证：
；
边上有且只有一个点
，使得
，求此时二面角
的余弦值.