摘要:解:(I)证明: 是以为首项.2为公比的等比数列. 得 (III)证明: ① ② ②-①.得--10分 即 ③ ④ ④-③.得 即是等差数列.
网址:http://m.1010jiajiao.com/timu_id_4398088[举报]
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若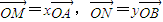 .
.
(1)求证:x与y的关系为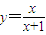 ;
;
(2)设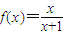 ,定义函数
,定义函数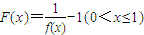 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令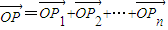 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得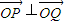 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程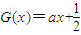 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
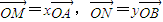 .
.(1)求证:x与y的关系为
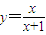 ;
;(2)设
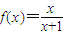 ,定义函数
,定义函数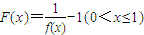 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令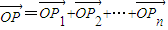 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得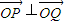 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程
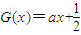 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.查看习题详情和答案>>
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若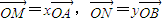 .
.
(1)求证:x与y的关系为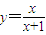 ;
;
(2)设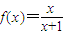 ,定义函数
,定义函数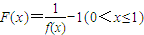 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令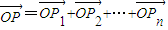 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得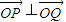 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程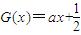 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
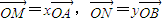 .
.(1)求证:x与y的关系为
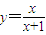 ;
;(2)设
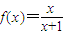 ,定义函数
,定义函数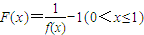 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令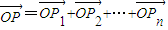 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得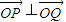 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程
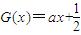 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.查看习题详情和答案>>
已知数列 满足
满足 (I)求数列
(I)求数列 的通项公式;
的通项公式;
(II)若数列 中
中 ,前
,前 项和为
项和为 ,且
,且 证明:
证明:
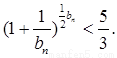
【解析】第一问中,利用 ,
,
∴数列{ }是以首项a1+1,公比为2的等比数列,即
}是以首项a1+1,公比为2的等比数列,即
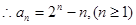
第二问中,

进一步得到得 即
即
即 是等差数列.
是等差数列.
然后结合公式求解。
解:(I) 解法二、 ,
,
∴数列{ }是以首项a1+1,公比为2的等比数列,即
}是以首项a1+1,公比为2的等比数列,即
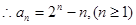
(II)
 ………②
………②
由②可得: …………③
…………③
③-②,得 即
即 …………④
…………④
又由④可得 …………⑤
…………⑤
⑤-④得
即 是等差数列.
是等差数列.




查看习题详情和答案>>
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若
=x
,
=y
.
(1)求证:x与y的关系为y=
;
(2)设f(x)=
,定义函数F(x)=
-1(0<x≤1),点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
的等比数列,O为原点,令
=
+
+…+
,是否存在点Q(1,m),使得
⊥
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
| OM |
| OA |
| ON |
| OB |
(1)求证:x与y的关系为y=
| x |
| x+1 |
(2)设f(x)=
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
| 1 |
| 2 |
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若
=x
,
=y
.
(1)求证:x与y的关系为y=
;
(2)设f(x)=
,定义函数F(x)=
-1(0<x≤1),点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
的等比数列,O为原点,令
=
+
+…+
,是否存在点Q(1,m),使得
⊥
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
| OM |
| OA |
| ON |
| OB |
(1)求证:x与y的关系为y=
| x |
| x+1 |
(2)设f(x)=
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
| 1 |
| 2 |