题目内容
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若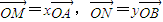 .
.(1)求证:x与y的关系为
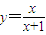 ;
;(2)设
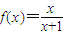 ,定义函数
,定义函数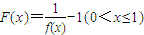 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令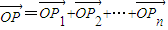 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得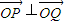 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程
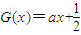 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
【答案】分析:(1)由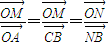 ,知
,知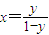 ,所以
,所以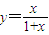 .
.
(2)由已知条件得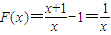 ,
,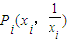 ,又
,又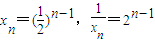 ,
,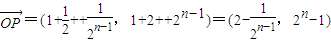 .由此可以推出存在
.由此可以推出存在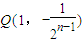 满足条件.
满足条件.
(3)由题意知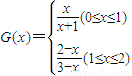 .由G(x+2)=G(x)得
.由G(x+2)=G(x)得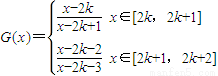 .同由此能够推出实数a的取值范围.
.同由此能够推出实数a的取值范围.
解答:解:(1)∵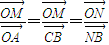 ,
,
∴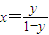 ,从而
,从而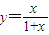 .
.
(2)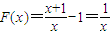 ,
,
∴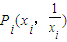 ,又
,又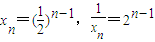 ,
,
∴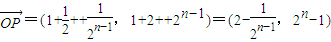 .
.
设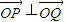 ,则
,则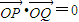 .
.
∴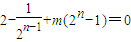 ,
,
∵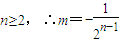 ,
,
故存在 满足条件.
满足条件.
(3)当x∈[0,1]时,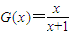 ,
,
又由条件得G(2-x)=G(x),
∴G(2+x)=G(-x)=G(x).
当x∈[1,2]时, ,
,
∵G(2-x)=G(x),
∴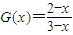 ,从而
,从而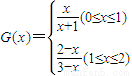 .
.
由G(x+2)=G(x)得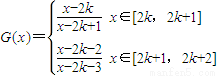 .
.
设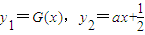 ,在同一直角坐标系中作出两函数的图象,
,在同一直角坐标系中作出两函数的图象,
当函数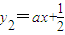 图象经过点(2k+2,0)时,
图象经过点(2k+2,0)时,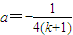 .
.
由图象可知,当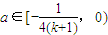 时,y1与y2的图象在x∈[2k,2k+2](k∈N)有两个不同交点,
时,y1与y2的图象在x∈[2k,2k+2](k∈N)有两个不同交点,
因此方程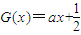 在x∈[2k,2k+2]上有两个不同的解.
在x∈[2k,2k+2]上有两个不同的解.
点评:本题考查数列的综合运用,解题时要深入挖掘题设中的隐藏含条件.
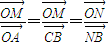 ,知
,知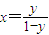 ,所以
,所以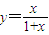 .
.(2)由已知条件得
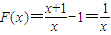 ,
,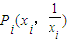 ,又
,又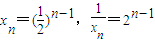 ,
,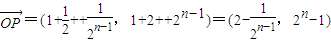 .由此可以推出存在
.由此可以推出存在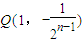 满足条件.
满足条件.(3)由题意知
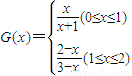 .由G(x+2)=G(x)得
.由G(x+2)=G(x)得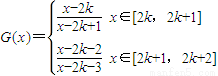 .同由此能够推出实数a的取值范围.
.同由此能够推出实数a的取值范围.解答:解:(1)∵
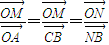 ,
,∴
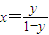 ,从而
,从而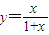 .
.(2)
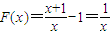 ,
,∴
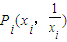 ,又
,又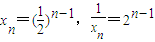 ,
,∴
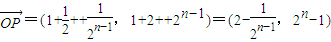 .
.设
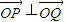 ,则
,则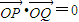 .
.∴
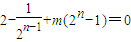 ,
,∵
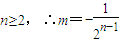 ,
,故存在
 满足条件.
满足条件.(3)当x∈[0,1]时,
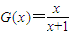 ,
,又由条件得G(2-x)=G(x),
∴G(2+x)=G(-x)=G(x).
当x∈[1,2]时,
 ,
,∵G(2-x)=G(x),
∴
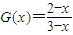 ,从而
,从而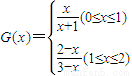 .
.由G(x+2)=G(x)得
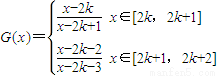 .
.设
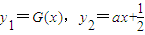 ,在同一直角坐标系中作出两函数的图象,
,在同一直角坐标系中作出两函数的图象,当函数
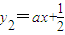 图象经过点(2k+2,0)时,
图象经过点(2k+2,0)时,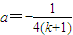 .
.由图象可知,当
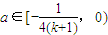 时,y1与y2的图象在x∈[2k,2k+2](k∈N)有两个不同交点,
时,y1与y2的图象在x∈[2k,2k+2](k∈N)有两个不同交点,因此方程
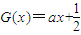 在x∈[2k,2k+2]上有两个不同的解.
在x∈[2k,2k+2]上有两个不同的解.点评:本题考查数列的综合运用,解题时要深入挖掘题设中的隐藏含条件.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
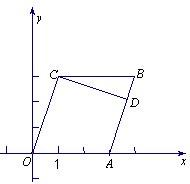 如图,在平行四边形OABC中,点C(1,3).
如图,在平行四边形OABC中,点C(1,3). 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点. 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.