摘要： 如图.某市拟在长为8km的道路OP的一侧修建一条运动 赛道.赛道的前一部分为曲线段OSM.该曲线段为函数 y=Asinx(A>0, >0) x[0,4]的图象.且图象的最高点为 S(3.2),赛道的后一部分为折线段MNP.为保证参赛 运动员的安全.限定MNP=120 (I)求A , 的值和M.P两点间的距离, (II)应如何设计.才能使折线段赛道MNP最长?
网址：http://m.1010jiajiao.com/timu_id_4395140[举报]
（2009福建卷理）（本小题满分13分）
已知A,B 分别为曲线C： 
+
=1（y
0,a>0）与x轴
的左、右两个交点，直线
过点B,且与
轴垂直，S为上
异于点B的一点，连结AS交曲线C于点T.
(1)若曲线C为半圆，点T为圆弧
的三等分点，试求出点S的坐标；
（II）如图，点M是以SB为直径的圆与线段TB的交点，试问：是否存在
,使得O,M,S三点共线？若存在，求出a的值，若不存在，请说明理由。 
（2009福建卷理）（本小题满分13分）
已知A,B 分别为曲线C： 
+
=1（y
0,a>0）与x轴
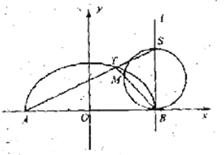的左、右两个交点，直线
过点B,且与
轴垂直，S为上
异于点B的一点，连结AS交曲线C于点T.
(1)若曲线C为半圆，点T为圆弧
的三等分点，试求出点S的坐标；
（II）如图，点M是以SB为直径的圆与线段TB的交点，试问：是否存在
,使得O,M,S三点共线？若存在，求出a的值，若不存在，请说明理由。
（2009福建卷理）（本小题满分13分）
如图，某市拟在长为8km的道路OP的一侧修建一条运动
赛道，赛道的前一部分为曲线段OSM，该曲线段为函数
y=Asin
x(A>0, >0) x
[0,4]的图象，且图象的最高点为
S(3，2
)；赛道的后一部分为折线段MNP，为保证参赛
运动员的安全，限定
MNP=120
（I）求A , 的值和M，P两点间的距离；
（II）应如何设计，才能使折线段赛道MNP最长？ 
赛道，赛道的前一部分为曲线段OSM，该曲线段为函数
x(A>0, 
[0,4]的图象，且图象的最高点为
)；赛道的后一部分为折线段MNP，为保证参赛
MNP=120
赛道，赛道的前一部分为曲线段OSM，该曲线段为函数
x(A>0, 
[0,4]的图象，且图象的最高点为
)；赛道的后一部分为折线段MNP，为保证参赛
MNP=120