摘要：2．.∴ 当或时..当时. ∴函数在和上是增函数.在上是减函数． ∴当时.函数取得极大值. 当时.函数取得极小值． 说明:解题的成功要靠正确思路的选择．本题从逆向思维的角度出发.根据题设结构进行逆向联想.合理地实现了问题的转化.使抽象的问题具体化.在转化的过程中充分运用了已知条件确定了解题的大方向．可见出路在于“思想认识 ．在求导之后.不会应用的隐含条件.因而造成了解决问题的最大思维障碍．
网址：http://m.1010jiajiao.com/timu_id_4393070[举报]
已知
，函数
（1）当
时，求函数
在点(1，
)的切线方程；
(2)求函数在[－1，1]的极值；
(3)若在
上至少存在一个实数x0，使
>g(xo)成立，求正实数
的取值范围。
【解析】本试题中导数在研究函数中的运用。（1）中
，那么当时，
又 
所以函数在点(1，)的切线方程为
；（2）中令
有 
对a分类讨论
，和
得到极值。（3）中，设
，
，依题意，只需
那么可以解得。
解：（Ⅰ）∵
∴
∴ 当时， 又
∴ 函数在点(1，)的切线方程为 --------4分
（Ⅱ）令 有
①
当
即时
|
|
（－1，0） |
0 |
（0， |
|
（ |
|
|
+ |
0 |
－ |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
）
故的极大值是
，极小值是
②
当
即时，在（－1,0）上递增，在（0,1）上递减，则的极大值为
，无极小值。
综上所述 时，极大值为，无极小值
时 极大值是，极小值是 ----------8分
（Ⅲ）设，
对
求导，得
∵
， 
∴ 在区间
上为增函数，则
依题意，只需，即
解得 
或
（舍去）
则正实数的取值范围是（
，
）
查看习题详情和答案>>
已知函数f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，当x＞0时，f（x）=log2x
（1）求当x＜0时，求函数f（x）的表达式
（2）若g（x）=2x（x∈R）集合A={x|f（x）≥2}，B={x|g（x）≥16或
≤g(x)≤1}，试判断集合A和B的关系．
查看习题详情和答案>>
（1）求当x＜0时，求函数f（x）的表达式
（2）若g（x）=2x（x∈R）集合A={x|f（x）≥2}，B={x|g（x）≥16或
| ||
| 2 |
已知函数f(x)=log
x，
（1）当x∈[
，3]时，求f（x）的反函数g（x）；
（2）求关于x的函数y=[g（x）]2-2ag（x）+3（a≤3）当x∈[-1.1]时的最小值h（a）；
（3）我们把同时满足下列两个性质的函数称为“和谐函数”：
①函数在整个定义域上是单调增函数或单调减函数；
②在函数的定义域内存在区间[p，q]（p＜q）使得函数在区间[p，q]上的值域为[p2，q2]．
（Ⅰ）判断（2）中h（x）是否为“和谐函数”？若是，求出p，q的值或关系式；若不是，请说明理由；
（Ⅱ）若关于x的函数y=
+t（x≥1）是“和谐函数”，求实数t的取值范围．
查看习题详情和答案>>
| 1 |
| 3 |
（1）当x∈[
| 1 |
| 3 |
（2）求关于x的函数y=[g（x）]2-2ag（x）+3（a≤3）当x∈[-1.1]时的最小值h（a）；
（3）我们把同时满足下列两个性质的函数称为“和谐函数”：
①函数在整个定义域上是单调增函数或单调减函数；
②在函数的定义域内存在区间[p，q]（p＜q）使得函数在区间[p，q]上的值域为[p2，q2]．
（Ⅰ）判断（2）中h（x）是否为“和谐函数”？若是，求出p，q的值或关系式；若不是，请说明理由；
（Ⅱ）若关于x的函数y=
| x2-1 |
已知函数f1（x）=lg|x-p1|，f2（x）=lg（|x-p2|+2）（x∈R，p1，p2为常数）
函数f（x）定义为对每个给定的实数x（x≠p1），f(x)=
（1）当p1=2时，求证：y=f1（x）图象关于x=2对称；
（2）求f（x）=f1（x）对所有实数x（x≠p1）均成立的条件（用p1、p2表示）；
（3）设a，b是两个实数，满足a＜b，且p1，p2∈（a，b），若f（a）=f（b）求证：函数f（x）在区间[a，b]上单调增区间的长度之和为
．（区间[m，n]、（m，n）或（m，n]的长度均定义为n-m）
查看习题详情和答案>>
函数f（x）定义为对每个给定的实数x（x≠p1），f(x)=
|
（1）当p1=2时，求证：y=f1（x）图象关于x=2对称；
（2）求f（x）=f1（x）对所有实数x（x≠p1）均成立的条件（用p1、p2表示）；
（3）设a，b是两个实数，满足a＜b，且p1，p2∈（a，b），若f（a）=f（b）求证：函数f（x）在区间[a，b]上单调增区间的长度之和为
| b-a |
| 2 |
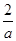